Inscription / Connexion Nouveau Sujet
Radioactivité - désintégrations successives
Bonjour !
je fais actuellement un exercice de physique issu d'un manuel mais j'ai vraiment du mal à le résoudre : serait-il possible d'avoir de l'aide ? merci !
énoncé:
"L'élément X est radioactif alpha, de constante radioactive lambda.
Le noyau fils Y est lui-même radioactif alpha, de constante de radioactivité lambda prime différente de lambda.
Dans une enceinte fermée, on isole un échantillon contenant N noyaux X et aucun noyau Y. On note x(t) la population en noyau X, y(t) la population en noyaux Y, n(t) le nombre total de noyaux d'hélium émis depuis l'instant initial et A(t) l'activité totale du système isolé à la date t."
Les questions sont en pièce jointe. A la question a, j'ai trouvé dx = x(t+dt) - xo e^(-lambda t) mais je ne suis vraiment pas sûre de ma réponse. Je bloque sur le reste des questions
Merci d'avance pour votre aide !
Bonjour ,
Je ne vois pas de différence entre votre exercice et la filiation radioactive à 2 corps traité dans les cours .
Voyez si ceci peut vous aider :
Bonjour ,
Je ne vois pas de différence entre votre exercice et la filiation radioactive à 2 corps traité dans les cours .
Voyez si ceci peut vous aider :
bonjour! merci beaucoup pour votre réponse, ce lien est très utile
ça m'a débloquée pour les questions 1a,b,c,d , mais je me retrouve de nouveau bloquée à la question 2 : je n'arrive pas à prouver que y(t) est bien solution, le lambda/(lambda' - lambda) m'embête dans mes calculs
Bonjour ,
Je ne vois pas de différence entre votre exercice et la filiation radioactive à 2 corps traité dans les cours .
Voyez si ceci peut vous aider :
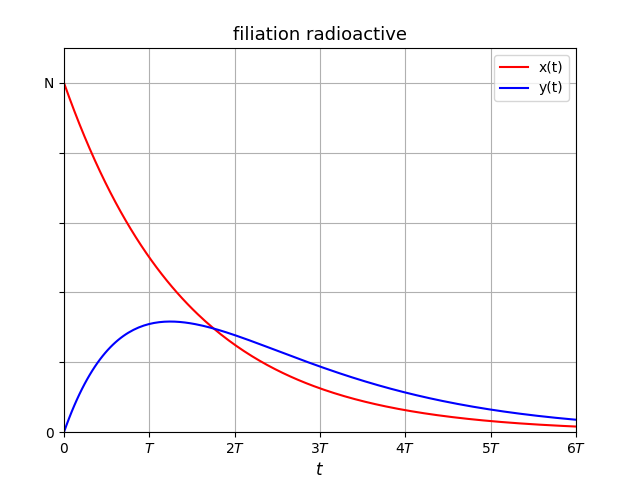
et pour la question 3, j'ai tracé les courbes en prenant des valeurs arbitraires puisqu'on ne nous en donnait aucune pour les tracer : c'est correct ?
j'obtiens quelque chose comme ça : [voir pièce jointe]
pour la question 4 j'ai trouvé A(t) = dx/dt + dy/dt = -(lambda')y. Pourriez-vous me dire si c'est juste s'il vous plaît ?
merci beaucoup à vous!
Bonjour
Je ne connais pas ton programme. Je ne sais donc pas si cette remarque préliminaire peut être utile. Cette étude de la filiation radioactive présente une forte analogie avec l'étude cinétique de deux réactions chimiques du premier ordre.
Question 1 : la variation élémentaire de x est bien :
dx=x(t+dt)-x(t)
mais ce n'est pas le résultat attendu : relis bien l'énoncé. Il suffit d'écrire que la quantité élémentaire de noyaux X disparue entre t et t+dt est :
.x.dt
Cela conduit d'ailleurs à l'équation 1 de la question 1.d)
Pour la question 2 : je te donne les pistes de calcul sans terminer ceux-ci.
Il faut d'abord calculer la dérivée de y par rapport à t :
Il faut comparer ce résultat à :
Pour la question 3 : il faut partir de la dérivée dy/dt fournie en 1.d (relation II) et remplir un tableau de variation pour montrer que y(t) passe bien par un maximum au cours de temps
Concernant les courbes :
1° : y(t) représente le nombre de noyaux Y présents à l'instant de date t. Cette valeur ne peux être négative et vaut zéro si t=0 selon l'énoncé.
2° : pour plus de clarté, il faut adapter l'échelle des abscisses à la valeur de la période T radioactive (demie-vie) de X.
J'ai tracé les deux courbes dans le cas particulier :
T'=0,75T soit '=(4/3)
Question 4 : comment justifies-tu l'expression de l'activité que tu fournis ?
Annuler
connectez vous