Bonjour
Comme d'habitude, une fois choisis le système et le repère, faire l'inventaire des forces et appliquer la relation fondamentale de la dynamique. Tu as résolu beaucoup plus difficile récemment...

D'accord je vais essayer, mais la présence de m'effraie. Je n'ai jamais étudié pareil en projectile.
Les problèmes que j'ai corrigé en projectile, seul le poids est appliqué (chute libre). Mais je vais tenter !

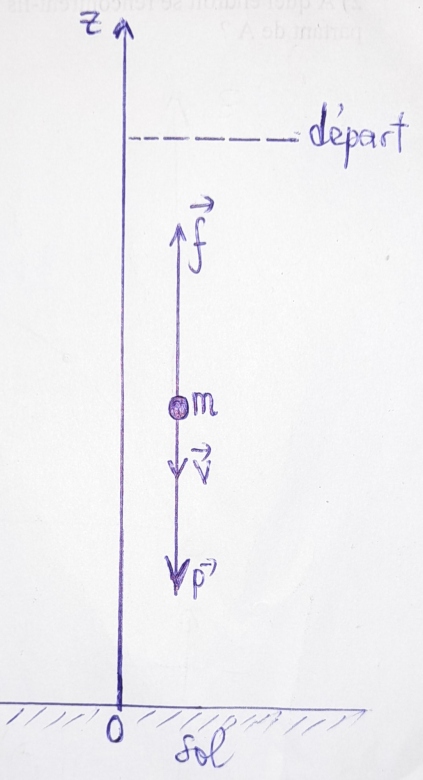
Tu peux faire un schéma soigné avec représentation du vecteur vitesse et des vecteurs forces.
Compte tenu de l'expression du vecteur force de frottement, que dire de la direction et du sens de cette force ?

D'accord, je commence à comprendre.
k étant positive, est colinéaire à mais de sens opposé.

Oui. Fais le schéma et projète la relation fondamentale de la dynamique sur l'axe vertical.

Voici ma démarche
1) Équation différentielle de la vitesse
- système : masse m ;
- référentiel : terrestre (supposé galiléen);
- bilan des forces : et  
(Figure)
TCI :

Sur l'axe Oz orienté vers le haut, on a :
- P + f = m.a
- mg + kV = m.V' V' - (k/m)V + g = 0

C'est mon dessin

2) Vérification



Donc

Sauf que quand je remplace v et v' dans l'équation différentielle je trouve ceci :

D'accord avec ta représentation des vecteurs mais il faut réfléchir à l'orientation de l'axe. Le sens du mouvement étant connu, il est préférable de l'orienter dans ce sens, donc ici vers le bas. Cela évite de manipuler un grand nombre de valeurs négatives, souvent sources d'erreurs de calcul mais il y a un argument encore plus fort. La solution attendue est :



Au bout d'une durée d'environ , l'exponentielle devient négligeable, la vitesse devient pratiquement constante et égale à : . C'est une valeur positive ; pour avoir une vitesse algébrique positive lors d'un mouvement vers le bas, il faut bien que l'axe (Oz) soit orienté vers le bas. La projection sur cet axe de la relation fondamentale de la dynamique conduit à :



Je te laisse continuer...

En orientant l'axe vers le bas, je trouve

V' + (k/m)V - g = 0

Oui !
Tu peux maintenant partir de l'expression proposée par l'énoncé et déterminer C à partir des conditions initiales.
Tu dérives ensuite par rapport au temps pour obtenir v' et tu vérifies que l'expression proposée est bien solution de l'équation différentielle.

Ah là ça marche maintenant !
J'ai dérivé l'expression de v donnée puis j'ai remplacé dans l'équation différentielle, j'ai trouvé 0.

Maintenant, à t = 0, v₀ = mg/k + C

Donc

C'est cela !

Question 3)
Je ne sais pas comment montrer que la vitesse tend vers une valeur limite V_L.

Mais, pour calculer cette vitesse limite,  je cherche la limite de V quand t tend vers l'infini.
Je trouve v = mg/k

Donc V_L = mg/k

Il te suffit, à mon avis sans refaire la démonstration, d'utiliser le résultat suivant de ton cours de math :

Merci bien mon cher

Cela ne semble pas demandé par l'énoncé mais il serait intéressant, sans faire de calcul mais en réfléchissant un peu à l'évolution des différentes grandeurs au cours de la chute libre, d'obtenir directement l'expression de la vitesse limite.

J'ai bien compris, merci !