Inscription / Connexion Nouveau Sujet
Projectile et artilleur
Bonjour, je planche sur un exercice. Aidez-moi svp.
Problème
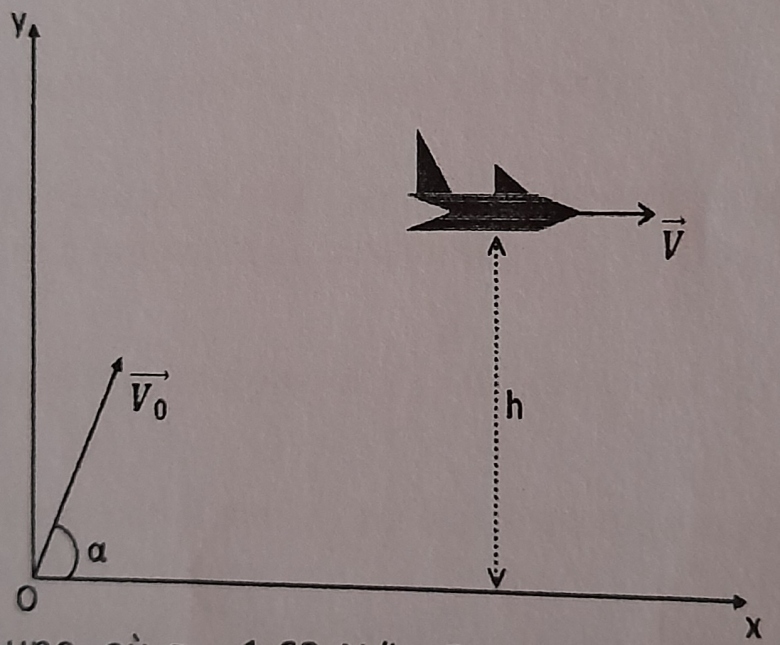
A l'aide d'un canon lançant un obus à une vitesse V0 = 300 m/s, un artilleur au sol veut atteindre un avion qui passe au-dessus de sa tête à une vitesse V = 1 080 km/h à une altitude h = 3 125 m. On néglige les frottements.
1) Établir les équations paramétriques du mouvement de l'obus. Écrire l'équation de la trajectoire de l'obus.
2) Montrer que le canon doit avoir une inclinaison minimale de 55,6⁰ pour que l'obus puisse atteindre l'avion.
3) Pour cette inclinaison minimale, déterminer les coordonnées du point de rencontre entre l'obus et l'avion. Où se trouve l'avion lors du départ de l'obus ?
4) L'angle de tir minimal serait-il le même sur la Lune, où g = 1,62 N/kg ? Sinon, serait-il plus élevé ou plus petit ? Expliquez !
Question 1 : application directe du cours
Je trouve :
et
La trajectoire est :
Question 2 : c'est là je suis bloqué
Voici mon raisonnement :
• les équations horaires de l'avion sont :
et
• L'obus atteint l'avion si xG = xA ou encore yG = yA
Mais, sauf qu'en posant xG = xA, je trouve
(Vcos )t = Vt
)t = Vt
J'obtiens cos = 1 ce qui n'est pas vrai !
= 1 ce qui n'est pas vrai !
En posant aussi yG = yA, je n'obtiens pas  = 55,6⁰
= 55,6⁰
Bonjour
On trouve souvent des éléments de réponse aux premières questions par la lecture des questions suivantes, d'où l'importance de lire un énoncé en entier avant de commencer la résolution.
La question 3 laisse clairement supposer que l'avion n'est pas nécessairement à la verticale du canon à l'instant du tir de l'obus...
Oui j'ai pensé à ça ! C'est-à-dire, l'avion n'est pas à la verticale du canon à l'instant où le projectile est tiré. Cet instant est pris comme origine des temps.
J'ai aussi essayé de trouver la durée nécessaire pour atteindre l'avion, là encore j'ai pas pu.
Pour la question 2, je pense qu'il suffit de déduire des résultats de la question 1 l'altitude maximale ymax , que peut atteindre l'obus, ymax étant une expression de Vo, g et  .
.
Une condition nécessaire à la réussite du tir étant alors : ymax > h.
Bien sûr, cette condition n'est pas suffisante mais cela est étudié ensuite.
Avec cette condition là, h = 3125 m représente la flèche de tir alors.
D'accord, en cherchant la flèche, on trouve :
AN : je trouve  = 55,58⁰
= 55,58⁰
Soit 
 55,6⁰
55,6⁰
Question 3
La rencontre a lieu au sommet de la parabole d'ordonnée y = h = 3125 m.
Maintenant je cherche la durée nécessaire mis par le projectile pour atteindre le sommet. Connaissant cette durée, je remplace dans l'équation de L'abscisse du projectile. C'est ça ?
C'est-à-dire, L'abscisse du sommet est égale à la portée du tir divisée par 2.
x = d/2 où d = V0²sin(2 )/g
)/g
Donc x = (V0²sin2 )/(2g)
)/(2g)
AN : x = 4269 m
Donc les coordonnées du point de rencontre sont :
x = 4269 m et y = 3125 m
D'accord avec ton raisonnement littéral. Je n'obtiens pas tout à fait la même valeur numérique de x.
Où se trouve l'avionlors du départde l'obus ?
• Je calcule la durée nécessaire du projectile pour atteindre x = 4282 m :
xG = V0cos t
t  t = x/(V0cos
t = x/(V0cos )
)
AN : t = 4282/(300cos55,85⁰) = 25,39 s
• Pendant cette durée (t=25,39 s) l'avion a parcouru xA = Vt = 300(25,39)
xA = 7618 m.
La différence de ces deux abscisses donne :
X = 7618 - 4282 = 3336 m
Alors l'avion était à un point B de coordonnées :
X = 3336 km, y = h = 3125 m. C'est ça ?
Réfléchis : l'avion et l'obus ont même vitesse. Pour avoir une chance d'atteindre l'avion, il faut tirer l'obus avant que l'avion ne passe à la verticale du canon. À l'instant du tir de l'obus, l'avion est bien à gauche de la verticale du canon (orientation du schéma).
D'accord, donc L'abscisse du point cherché est :
x = xG - xA à t = 24,39 s
x = 4282 - 7618 = - 3336 m
Donc l'avion était en un point B de coordonnées
xB = -3336 m ; yB = h = 3125 m
C'est ça ?
D'accord avec ton raisonnement littéral. Étourderie semble-t-il dans l'application numérique : la date de collision est passée de 25,39 à 24,39s.
D'accord pour t = 25,39s. Mais cela ne change pas les coordonnées de B.
xB = -3336 m ; yB = h = 3125 m
C'est ça ?
Acceptable je pense. Attention tout de même : s'il faut arrondir les résultats demandés en fonction de la précision des données, il est prudent de conserver tous les chiffres de la calculatrice dans la suite des calculs ; sinon, les arrondis successifs peuvent finir par générer des erreurs.
Ici, par exemple, avec les données fournies et g=9,81m/s2, j'obtiens :
 =55,6269...
=55,6269... 55,6°
55,6°
x=4275,1549... 4275m
4275m
xB=-3297,1267... -3297m
-3297m
Merci !
Question 4
Sur la lune, g = 1,62 N/kg
La flèche est
Je trouve  ' = 19,597⁰
' = 19,597⁰
Soit
L'angle est plus petit !
Je ne sais pas le "pourquoi"
On suppose h constant. Puisque la vitesse de l'obus est imposée, la seule façon de maintenir l'expression de h constante sachant que le dénominateur diminue est de diminuer également le numérateur. Puisque Vo est imposée, il faut diminuer l'angle de tir.


