Inscription / Connexion Nouveau Sujet
projectile
Bonjour,
J'aurais besoin d'aide sur cet exo,
Dans tout le problème on négligera les frottements et on prendra g=10 m/s2.
La piste de lancement d'un projectile M est situé dans un plan vertical : elle comprend une partie rectiligne ABC horizontal et une portion CD qui est un demi-cercle de centre O et de rayon r=1m.
Le projectile M de masse m=0,5 kg, est initialement au repos en A. On le lance sur la piste en faisant agir sur lui, le long de la partie AB de sa trajectoire une force horizontal et d'intensité F constante. On pose AB=l=1,5m et BC=5m.
Au point M défini par l'angle (OC,OM)=
. Établir en fonction de F,l,r,m,g et l'expression de :
a)La valeur V de la vitesse du projectile.
b) l'intensité R de la réaction de la piste.
Merci d'avance !
Travail de la force F sur le trajet AB : W = F * L
En B, ce travail a été transformé en énergie cinétique de la masse m --->
F * L = 1/2.m.(VB)²
(VB)² = 2F.L/m
VB = RC[2L.F/m]
Sur le trajet BC, comme les frottements sont négligeables, le projectile est en MRU, sa vitesse est constante
Et donc VC = VB
VC = RC[2L.F/m]
--------
A toi pour la suite ...
- Quelle est la différence d'altitude entre le point C et le point M (en fonction de r et de theta) ?
- Quel est le travail du poids du projectile sur le trajet CM ?
- A partir des réponses précédentes, quelle est l'énergie cinétique du projectile en M (pense à la conservation de l'énergie mécanique)
- Et donc, à partir de la réponse à la ligne précédente, quelle est la vitesse du projectile en M ?
...
Essaie. 
La différence d'altitude entre C et M est z=r×.
Le travail du poids du projectile sur CM est
W=mgr.
A l'absence des frottements l'énergie mécanique se conserve :
E(C)=E(M)
Ec(C)+Epp(C)=Ec(M)+Epp(M)
Ec(M)=Ec(C)+Epp(C)-Epp(M).
Mais je ne sais pas comment effectué cette calcul.
La différence d'altitude entre C et M est z=r×
.
Ce n'est pas correct.
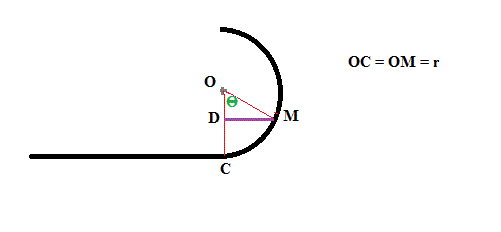
OC = r
OD = OM.cos(theta) = r.cos(theta)
DC = OC - OD = r - r.cos(theta) = r.(1 - cos(theta))
Et DC est la différence d'altitude entre C et M
Ce qui est différent de ce que tu avais écrit.
-----
Corrige la suite en conséquence.
Le travail du poids sur BC est:
W=Pr(1-cos)
W=mgr(1-cos).
Ec(C)+Epp(C)=Ec(M)+Epp(M)
Ec(M)=Ec(C)+Epp(C)-Epp(M)
Ec(M)=
)" alt="\frac{1}{2}m×\frac{2}{m}F×l+mgr(1-cos
)" class="tex" />
)" alt="\frac{1}{2}mVM^2=F×l+mgr(1-cos
)" class="tex" />
il vient donc :
))" alt="VM=√(\frac{2}{m}F×l+2gr(1-cos
))" class="tex" />.
Est-ce que c'est bon?
- force centrifuge sur le projectile en M (référentiel lié au projectile) : |Fc| = m.(vM)²/r
Et si on veut rester dans un référentiel terrestre (en considérant celui-ci comme galiléen) : Force centripète sur l'objet en M : | Fc| = m.(vM²)/r
Cette force ne peut être que due qu'à la réaction R du support sur le projectile et donc :
|R| = m.(vM²)/r, elle est normale au demi cercle en M et dirigée vers de M vers 0
Annuler
connectez vous