Inscription / Connexion Nouveau Sujet
Problème sur Induction électromagnétique
Bonsoir, s'il vous plait je voudrais de l'aide pour la dernière question de cet exercice. Merci
ÉNONCÉ
Une barre MM', homogène de masse m, peut glisser sans frottement le long des rails métalliques AC et A'C', espacés d'une distance l et contenus dans un plan incliné d'un angle 
par rapport au plan horizontal. Pendant tout le temps que dure le mouvement, la barre reste perpendiculaire aux rails et maintient entre eux le contact électrique en M et M'. Les points A et A' sont reliés par un conducteur ohmique de résistance R et un interrupteur K. L'ensemble du dispositif est plongé dans un champ magnétique uniforme vertical ascendant . On négligera dans tout l'exercice, l'influence du champ magnétique terrestre. On ferme le circuit et on abandonne la barre sans vitesse initiale en A et A' à l'instant t=0.
1. Établir, en fonction de la vitesse v de la barre, de B et l, l'expression de la f.é.m. induite dans le circuit
2. Préciser, sur un schéma, le sens de l'intensité i du courant qui le parcourt.
3. Déterminer la direction, le sens et l'expression de l'intensité f de la force magnétique qui agit sur la barre.
4 Montrer que la vitesse de la barre tend vers une valeur limite que l'on calculera.
Données : l=20cm ; g=10N/kg ; R= 0,1? ; B= 1T ; m= 20g ; = 30°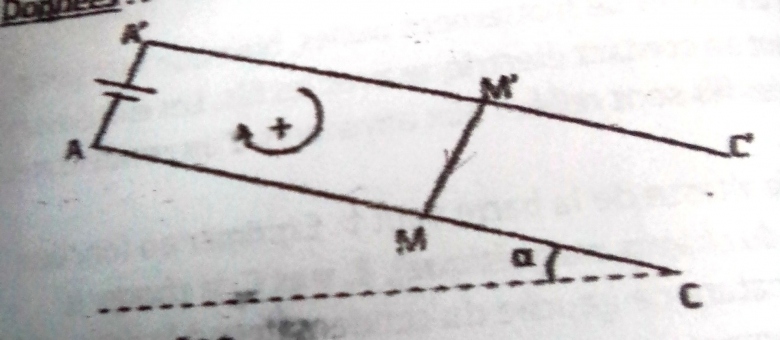
Bonsoir pfff,
Bienvenue sur l'
voisine !
Chez les physiciens, c'est pareil que pour les mathématiciens, on aime bien des pistes de réflexion pour démarrer l'échange 
.
Je suis sûr que tu as ta petite idée sur la question, par exemple faire le lien avec le cours (
[lien])
-------------------
Une fois que ce sera fait, un membre se fera un plaisir de t'accompagner dans sa résolution.
Bonne soirée, 
Mes réponses
1- e=Blvcosa
2- i va de M' vers M
3-Caractéristiques
Direction : Perpendiculaire à MN et B
Sens: de C vers A
Valeur : f= ilB
4- J'y arrive pas
Bonsoir,
Tu me sembles sur le bon chemin.
Utilise la 2e loi de Newton appliquée à la barre.
Projette l'expression vectorielle obtenue sur un axe descendant parallèle à AC sans oublier que i = e/R
Tu obtiens une équation différentielle concernant la vitesse.
Pour obtenir la vitesse limite Vlim , tu n'as pas besoin de résoudre cette équation.
Il suffit de remarquer que quand v(t) = Vlim on a aussi dv/dt = 0
Donc on a
F+P+R=ma
En projetant sur A'C' j'obtiens :
mgsina - F = ma
Mais je ne vois pas encore comment faire intervenir la vitesse
Intensité de la force de Laplace :
F = B i L avec
i = e / R et
e = B L v cos(α)
L'équation différentielle contient donc la vitesse "v" et sa dérivée dv/dt
Non :
Intensité de la force de Laplace :
F = B i L = B * ( B L v cos(α) / R) * L = B² L² v cos(α) / R
Projection de F sur l'axe AC = - F * cos(α) = - B² L² v cos² (α) / R
Projection du poids sur l'axe AC = m g sin(α)
Projection des réactions des rails sur l'axe AC = 0 ( si on néglige les frottements )
Je te laisse continuer.
Ah ok
-F+P+0 = m(dv/dt) 
- B² L² v cos² (α) + m g sin(α) = m(dv/dt)
lorque la vitesse de la barre tend vers une valeur limite V=
donc on a : - B² L² cos² (α) + m g sin(α) = m(d
/dt) or d
/dt = 0
donc on a : - B² L² cos² (α) + m g sin(α) = 0
B² L² cos² (α) = m g sin(α)
=
je trouve Vm = 3.33m/s
On y est presque :
Bizarrement la résistance R du circuit a disparu de ton calcul.
Voir mon post du 05-05-20 à 18:55
Remarque :
Lorsque la vitesse V(t) prend la valeur limite VL (qui est une constante) l'accélération dV/dt devient nulle.
On a donc dV / dt = 0 et non dVL / dt = 0
oups, je reprends
-F+P+0 = m(dv/dt) (- B² L² v cos² (α)) / R + m g sin(α) = m(dv/dt)
lorque la vitesse de la barre tend vers une valeur limite dv/dt=0
donc on a : (- B² L² cos² (α)) / R + m g sin(α) = m(d
/dt)
donc on a : (- B² L² cos² (α))/R + m g sin(α) = 0
(B² L² cos² (α)) / R = m g sin(α)
=
je trouve Vm = 0.33m/s
Vu que vous vous êtes déconnecté, je vous souhaite Bonne nuit.
Et j'espère que j'ai trouvé cette fois 
Annuler
connectez vous