Inscription / Connexion Nouveau Sujet
Problème sur Auto-Induction
Bonjour j'ai fait ce exercice et quand je regarde la correction, tout est différent. Merci de m'aider.
ÉNONCÉ
1. On considère une bobine assimilable à un solénoïde théorique ayant les caractéristiques suivantes :
. Rayon moyen des spires R=10cm
. Nombre total des spires N=500
. Longueur de la bobine l=1m
a. Déterminer les caractéristiques du vecteur champ magnétique B créé à l'intérieur de ce solénoïde lorsqu?il est parcouru par un courant d'intensité I=5A.
b. Calculer l'inductance du solénoïde.
2. L'intensité du courant qui circule dans la bobine est caractérisée successivement par les valeurs suivantes exprimées en ampères : =2 ;
= 5t + 2 ;
= 2
2 sin (100
.t) ; =
3 cos (50.t + ? )
Calculer la force électromotrice d'auto-induction produite dans chacun des cas.
3.Un courant d'intensité i(t) traverse la bobine (voir graphique)
a-Exprimer la tension aux bornes de la bobine en fonction du temps.
b-Représenter graphiquement . On prendra le sens positif du conducteur de M vers N et on négligera la résistance interne de la bobine.
Dans le prochain message je donne mes pistes de réflexions
***Edit gbm : le mieux serait de regrouper l'énoncé et la réflexion, cela ferait gagner du temps à tout le monde (cf. ton autre sujet avec odbugt1 qui attend toujours tes pistes)***
Ok Gbm
1- a-Caractéristiques
Direction : suivant l'axe de la bobine
Sens : du pôle sud vers le pôle nord
Valeur B = 3,14*
1-b- L = N²s / l
L= 9,87*10^-3
1-c Em = 1/2 Li²
Em = 1,23*10^-1
Je vous laisse vérifier cette première partie
Merci
Maintenant la 2.
On sait que e=-L(di/dt)
Donc e= -9,86*10^-3(di/dt)
. pour = 2, d
/dt =0
D'où e=0v
. pour =5t+2, d
/dt = 5
D'où e=-4,93.10^-2v
. pour =2√2 sin(100π.t) d
/dt = 2√2*100π cos(100π.t)
D'où e=-8,76 cos(100π.t)v
Le dernier j'y arrive pas
D'accord avec ce que tu as fait. Attention aux unités : di/dt se mesure en A/s et l'abréviation de volts est V majuscule car le nom de l'unité dérive du nom d'un scientifique : Volta.
Pour i4, la formule que tu as écrite fait apparaître un "?" . Peux-tu réécrire l'expression de i4 ?
A priori, si f(x) = A.cos(
.x+
) où et sont deux constantes, quelle est l'expression de la dérivée par rapport à x : f'(x) ? Je pense que tu as un problème analogue pour di4/dt.
Oui j'oublie a chaque fois. Merci beaucoup
= √3 cos(50π.t + φ )
Je n'arrive pas à faire la dérivée à cause du φ
3.Un courant d'intensité i(t) traverse la bobine (voir graphique)
a-Exprimer la tension aux bornes de la bobine en fonction du temps.
b-Représenter graphiquement . On prendra le sens positif du conducteur de M vers N et on négligera la résistance interne de la bobine.
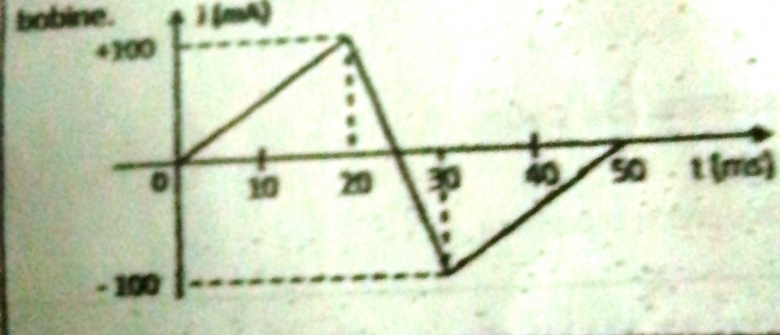
Peut-être ; pour être tout à fait sûr, il faudrait un schéma indiquant à la fois l'orientation de la bobine et les bornes M et N. Ce que tu as écrit correspond à la bobine orientée en convention "récepteur".
Pour la valeur de e, il suffit de déterminer les coefficients directeurs des différentes portions de courbe...
Annuler
connectez vous