Inscription / Connexion Nouveau Sujet
Problème avec projection sur axe x'x du vecteur accélération
Bonsoir,
un exemple d'application de la 2nde loi de Newton.
Imaginons qu'on ait par exemple :
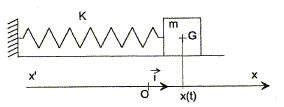
On obtiens vectoriellement :
avec
force de rappel du ressort.
je ne comprends pas ensuite, en projetant sur l'axe x'x pourquoi on n'a pas :
F=ma !?
Le vrai résultat est : -F=ma
je suis d'accord que la projection de sur x'x donne -F mais donc puisque les vecteurs sont colinéaires la projection de
sur x'x doit donner -a et pas a, non ?!
merci de m'aider c'est très obscur pour moi
Bonsoir,
Je pense que tu as simplement "raté" une étape.
Au passage, n'oublie pas dans un problème de mécanique, de définir le référentiel, le système étudié, et de faire un bilan des forces) :
Référentiel : terrestre, considéré comme Galiléen
Système : le solide (S) fixé au ressort
Bilan des forces : poids de (S) , réaction du support
, force de rappel du ressort
La seconde loi de Newton te donne :
On projette l'équation selon l'axe x'Ox :
on retrouve bien l'expression que tu proposes (on n'a pas explicité F).
Or la force F est peut s'exprimer comme , où k est la constante de rappel du ressort et x(t) la position de G par rapport à la position d'équilibre (si je lis bien ton schéma), et
le vecteur unitaire de l'axe x'Ox.
L'équation (1) devient :
,
et je pense que c'est ce qu'on a écrit et pas -F = ma ?? Est ce que je me trompe ?
Ta remarque : "la projection de sur x'x donne -F" n'est pas exacte. Si tu reprends l'expression de
(=-k x(t) i), tu vois que selon le signe de x(t),
et
sont dans le même sens (x(t)<0) ou dans le sens opposé (x(t)>0)!
J'espère que c'est plus clair maintenant.
Bonsoir nutsdz,
je te remercie grandement pour ta réponse qui m'a bien aidé.
Au passage, n'oublie pas dans un problème de mécanique, de définir le référentiel, le système étudié, et de faire un bilan des forces)
Je le fais c'est juste que j'ai mis le minimum minimorum pour ne pas effrayer d'éventuels correcteurs par la longueur du sujet ...

où k est la constante de rappel du ressort et x(t) la position de G par rapport à la position d'équilibre (si je lis bien ton schéma)
C'est parfaitement ça.
En effet j'avais tort ... je m'étais trompé en étant passé par
En fait la projection de
Donc merci beaucoup ça faisait un moment que j'avais du mal avec ça !
Salut,
Désolé de revenir sur une de tes remarques, mais
En fait la projection de
ce n'est pas correct.
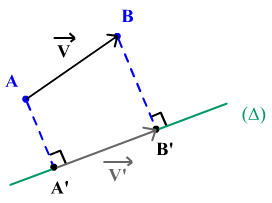
La projection d'un vecteur sur un axe est un vecteur (voir figure ci-dessous pour mémoire). Ici, on sait que l'expression de la force de rappel
Donc en projetant l'égalité
On remplace
Donc pour résumer :
la projection de
Peut être que quelqu'un d'autre peut essayer de t'éclairer, je suis à bout d'argument

Bonne soirée,
Ok merci je comprends merci de me faire part de mes erreurs.
Donc quand on passe d'une égalité vectorielle à une égalité non vectorielle, ça s'appelle comment ?
Une autre question : je vais peut-être dire une énorme bêtise mais, je pense que
Bonsoir,
Une autre question : je vais peut-être dire une énorme bêtise mais, je pense que
Heu pas forcément une énorme bêtise, mais c'est faux !
Tu as montré que
Il faut bien comprendre que x(t) représente la position de G par rapport à la position d'équilibre (c-a-d quand le ressort n'est ni comprimé ni étiré). Si tu étires le ressort (comme dans ton schéma), alors x(t) est positif, F sera négative (donc dirigé de x vers x') et a_x sera négatif (dirigée de x vers x').
Au contraire, si tu comprimes le ressort, alors x(t) sera négatif (avec l'orientation que tu as choisie).
Tu dois bien comprendre que dire F (ou a) est négative n'est pas très juste. C'est comme pour l'intensité du courant électrique dans un circuit : cela signifie que ton vecteur est dirigé dans le sens négatif par rapport à la convention que tu as choisie (ici, l'orientation de ton axe x'Ox) !!
Bon j'espère ne pas t'avoir trop embrouillé. Demande à ton prof de t'expliquer de vive voix, ça vaut peut être mieux.
Oui pardon dans ma tête je pensais a(t) négative avec en même temps x(t) positive (c'est-à-dire que le ressort est étiré). Après (lorsque la position d'équilibre est dépassée et le ressort cette fois-ci comprimé) bien-sûr les signes changent.
Je préfère ne pas trop m'expliquer là-dessus, mais c'est le fait que a(t) et x(t) ne soient pas constantes puisqu'en fonction du temps (donc leur signe change) qui m'embrouillait au début ...
En fait, en fonction que le ressort soit étiré/comprimé, le vecteur est dirigé vers la droite/gauche et je pensais que ce vecteur avait un sens qui ne changeait pas au cours du temps.
P.S. en espérant ne pas avoir écrit de bêtises, je précise évidemment que les signes sont en fonction de l'orientation de l'axe
P.P.S. tu expliques très bien ^^
Bonjour,
Content d'avoir pu t'aider... Si tout est clair maintenant c'est parfait.
Et merci pour le P.P.S., je transmettrai aux jurys qui vont m'évaluer 

Bonne journée,


