Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau terminale
Partager :

Poulie à deux cylindres

Posté par
fidele11 29-12-20 à 18:29

Bonsoir...
Pouvez-vous m'aider à traiter cet exercice dont l'énoncé est le suivant:


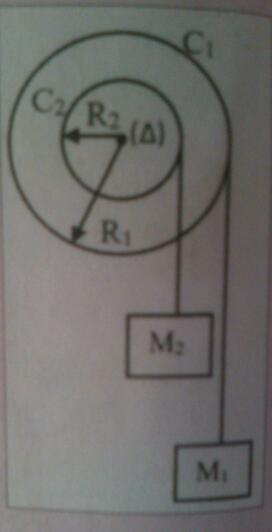
Une poulie formée de deux cylindres solidaires C1 et C2 coaxiaux de rayons R1=20 cm et R2=10cm , de masses respectives m1=2kg et m2=0,5kg (supposées réparties sur la périphérie ), peut tourner sans frottement autour d'un axe fixe horizontal (Delta).
1. On enroule sur le cylindre C1 un fil f1 à l'extrémité duquel est accroché une masse M1=150g. Sur le cylindre C2, on enroule dans le même sens, un fil f2, à l'extrémité duquel est accroché une masse M2=200g. Le système est abandonné sans vitesse initiale. Déterminer :
1.1) Le moment d'inertie de la poulie;
1.2) les accélérations linéaires a1 et a2 de M1 et M2;
1.3) L'accélération angulaire Ö de la poulie;  
1.4) La vitesse linaire de M1 après un parcours de 2m et le temps mis;
1.5) Les tensions T1 et T2 des fils f1 et f2.
2. Dans le dispositif ci contre, les mouvements de M1 et de M2 s'effectuent maintenant en sens incerses. Calculer :
2.1) les accélérations linéaires a1 et a2 de M1 et M2;
2.2) L'accélération angulaire Ö de la poulie;
2.3) les tensions T1 et T2 des fils f1 et f2.
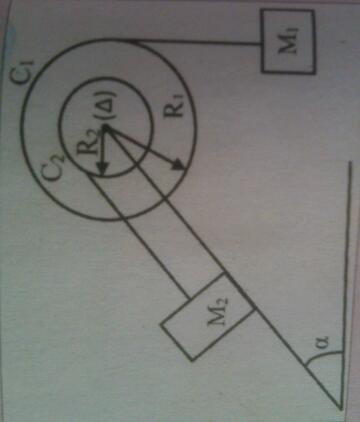
3. Sachant que dans ce   dispositif , la masse M2 repose sur un plan incliné d'un angle alpha=30° par rapport à l'horizontale (les frottements sont négligés ), Déterminer :
3.1) les accélérations linéaires a1 et a2 de M1 et M2;
3.2) L'accélération angulaire Ö de la poulie;  
3.3) Les tensions T1 et T2 des fils f1 et f2.

Mon début :
1.1) Ici,  j'ai fait la somme des moments d'inertie des cylindres qui constituent la poulie:
J=½*m1*R²[1] + ½*m2*R²[2]
=4,25*10^(-2) kg/m²
1.2)Accélérations linéaires :
Suivant le sens du mouvement (axe qu'on désignera par (Oy)),
Pour M1, En appliquant le TCI,
P-T1=m1*a1 => a1=(M1*g-T1)/M1
Pour M2, j'obtiens de même a2=(M2*g-T2)/M2.

1.3) accélération angulaire Ö de la poulie :
En appliquant la relation fondamentale de la dynamique,
M(T1)+M(T2)=J*Ö
=> -T1*R1-T2*R2=-JÖ
=> Ö=(T1*R1+T2*R2)/J

1.4) Vitesse linéaire de M1 après 2m.
L'accélération de M1 est a1=(M1-T1)/M1, Sa vitesse en fonction du temps est V1(t)=(M1*g-T1)t/M1,
J'aboutis à loi horaire:
y(t)=(M1*g-T1)t²/(2*M1),
L'l'équation du mouvement est :
y=(V²1*M1)/(2(M1*g-T1)).

J'aimerais donc calculer V1 pour y=2, mais je n'ai pas encore la tension qui est demandée à la question suivante...

Poulie à deux cylindres

Poulie à deux cylindres

Posté par
vanoisere : Poulie à deux cylindres 29-12-20 à 18:38

Bonsoir
Je pense qu'il faut aussi exprimer la vitesse angulaire de la poulie uniquement en fonction de g, des masses et des deux rayons.

Posté par
fidele11re : Poulie à deux cylindres 29-12-20 à 18:55

Qu'en est-il des deux accélérations linéaires, a1 et a2 ? La relation finale sera t-elle en fonction de ces accélérations?

Posté par
vanoisere : Poulie à deux cylindres 29-12-20 à 19:02

Petit indice pour t'aider : tu peux te poser la question suivante : quand les poulies tournent d'un angle , de quelle distance x1 descend la masse M1 et de quelle distance x2 descend la masse M2. En dérivant par rapport au temps, tu vas obtenir la vitesse angulaire \dot{\theta} en fonction de R1 et de v1 et cette même vitesse angulaire en fonction de R2 et v2. En dérivant une seconde fois par rapport au temps, tu vas obtenir l'accélération angulaire\ddot{\theta} en fonction de R1 et a1 puis en fonction de R2 et a2.

Posté par
fidele11re : Poulie à deux cylindres 29-12-20 à 19:57

Lorsque les poulies tournent d'un angle ∅, les masses descendent  de:
-2R1*sin(∅/2)
-2R2*sin(∅/2).
je ne sais pas s'il faut trouver deux relations de l'accélération angulaire de la poulie: l'une provenant de du cylindre C2 et l'autre du cylindre C1...
Pour le cylindre C1, a1=(M1*g-T1)/M1
on a également la relation ; a1=R1*Ö
De plus en appliquant la RFD à C1, T1R=J1*Ö
Puis-je utiliser ces relations pour obtenir une relation de Ö ?

Posté par
vanoisere : Poulie à deux cylindres 29-12-20 à 20:58

Il faut supposer les fils inextensibles et supposer qu'ils se déroulent sans glisser sur les cylindres. Quand  M1 descend de x1, le fil se déroule de la même longueur. Par définition même du radian :
x1=R1.
On montre de même :
x2=R2....

Posté par
fidele11re : Poulie à deux cylindres 29-12-20 à 21:18

vanoise @ 29-12-2020 à 18:38

exprimer la vitesse angulaire de la poulie uniquement en fonction de g, des masses et des deux rayons.
… Désolé, jusque là, je ne parviens vraiment pas à trouver cette expression

Posté par
vanoisere : Poulie à deux cylindres 29-12-20 à 22:55

a_{1}=R_{1}.\ddot{\theta} et a_{2}=R_{2}.\ddot{\theta}

La relation fondamentale de la dynamique appliquée à chacune des deux masses et le théorème des moments appliqué à la double poulie conduisent à trois expressions de \ddot{\theta}. Il suffit alors d'éliminer les deux tensions T1 et T2 entre ces trois relations pour obtenir l'accélération angulaire.

Posté par
fidele11re : Poulie à deux cylindres 30-12-20 à 14:16

Application de la RFD aux deux masses (systèmes étudiés dans un référentiel terrestre supposé galiléen ):
Masse 1:
\vec{P_1}+\vec{T_1}=M_{1}\vec{a_1}
<=> M_{1}g-T_{1}=M_{1}a_{1} De là, T1=M1*g-M1*a1
Masse 2:
Je trouve de même T2=M2*g-M2*a2

En appliquant de même le théorème des moments à la double poulie,
T_{1}R_{1}+T_{2}R_{2}=J*o^{..}{

L'accélération angulaire de la poulie est donc:
o^{..}=g\frac{M_{1}R_{1}+M_{2}R_{2}}{J+R^{2}_{1}M_{1}+R^{2}_{2}M_{2}}

L'accélération linéaire de la masse M1 est:
a1=R1*Ö
<=> a_{1}=R_{1}g\frac{M_{1}R_{1}+M_{2}R_{2}}{J+R^{2}_{1}M_{1}+R^{2}_{2}M_{2}}

En integrant a1 par rapport au temps successivement puis je obtenir la vitesse linéaire?

Posté par
vanoisere : Poulie à deux cylindres 30-12-20 à 14:38

Bravo ! Tout cela n'est pas évident !
D'accord avec tes expressions des accélérations.
Pour les vitesses : le plus simple consiste à utiliser les lois caractéristiques d'un mouvement rectiligne uniformément varié. N'oublie pas la troisième relation, souvent plus utile que les deux qui font intervenir le temps :
v2 - vo2=2a.(x-xo)

Posté par
fidele11re : Poulie à deux cylindres 30-12-20 à 15:10

Ainsi comme la vitesse initiale est nulle, V=\sqrt{2a_{1}(x-x_{0})} avec a1 l'accélération precedente et x-x_0=2 m, je peux appliquer cela?

Posté par
vanoisere : Poulie à deux cylindres 30-12-20 à 15:28

Oui. C'est à mon avis la méthode la plus rapide.  Pour te rassurer, tu peux vérifier qu'il est possible d'arriver au même résultat en calculant d'abord la durée du mouvement.

Posté par
fidele11re : Poulie à deux cylindres 30-12-20 à 15:57

Je trouve en application numérique a1=1,99 m/s²
V=2,81 m/s.

Posté par
fidele11re : Poulie à deux cylindres 30-12-20 à 15:59

V=d/t => t=d/V=0,71 s

Posté par
vanoisere : Poulie à deux cylindres 30-12-20 à 16:05

Erreur au dernier message.  V=d/t concerne uniquement les mouvements uniformes.

Posté par
fidele11re : Poulie à deux cylindres 30-12-20 à 16:15

oups, la vitesse varie ici en fonction du temps ... je dois donc trouver la loi horaire du mouvement ?

Posté par
fidele11re : Poulie à deux cylindres 30-12-20 à 16:22

a1≈2 m/s²
v(t)=2t + Vo
y(t)=t²+Vo*t + Yo
or Vo=0 m/s et Yo=0
<=> y(t)=t²  pour y=2 m : t=√2=1,41 s

Posté par
fidele11re : Poulie à deux cylindres 30-12-20 à 16:44

1-5) Tensions des fils
les accélérations a1 et a2 étant connues,
T1=M1*g-M1*a1=1,20 N
T2=M2*g-M2*a2=1,80 N

Posté par
vanoisere : Poulie à deux cylindres 30-12-20 à 17:44

message de 16h22 : puisque v1=a1.t tu obtiens bien une vitesse v2 de 2,82m/s, résultat obtenue directement par la méthode que j'ai indiquée, aux arrondis de calculs près.
Message de 16h44 : d'accord avec tes résultats.

Posté par
fidele11re : Poulie à deux cylindres 30-12-20 à 18:25

D'accord...
2. les mouvements de M1 et M2 s'effectuent maintenant. en sens inverses : je pense qu'il sera juste question d'un changement de signe de l'un des paramètres. Par exemple si la Masse M1 s'élève et M2 descend,
T1=M1*a1+M1*g et les autres expressions de la Q1 seront conservées.
3. Il en est de même pour ce dispositif,  juste que le poids sera exprimé en fonction de l'angle alpha,

Posté par
vanoisere : Poulie à deux cylindres 30-12-20 à 18:46

Effectivement, l'étude est analogue à la précédente avec un moment de T2 négatif et la prise en compte seulement de la composante du poids de M2 le long du plan incliné. Intuitivement, cela revient, dans l'expression des accélérations, à remplacer au numérateur  M2 par :
-M2.sin()
Je te laisse le vérifier.

Posté par
fidele11re : Poulie à deux cylindres 30-12-20 à 19:04

Oui exactement c'est bien cela.
Merci beaucoup à vous !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !