Inscription / Connexion Nouveau Sujet
physique mouvements de chutes verticales
bonjour a tous j'aimerai un petit peu d'aide svp pour un exercice de physique sur les mouvements de chutes verticales voici l'exercice:
un élève laisse tomber une bille en verre de rayon r=0.8cm dans l'eau d'une piscine. la profondeur de la piscine est h=1.70m, il trouve que la durée de la chute est voisine de 2.5s. données: masse volumiques: eau=1000kg.m^-3 verre=2500kg.m^-3 masse de la bille m=5.4g
1) effectuer le bilan des forces agissant sur la bille et l'équation différentielle du mouvement. la valeur de la force de frottement fluide: F= k.v² avec k=0.045 unitéS.I
2) a partir de l'équation différentielle, exprimer, avec des coefficients numeriques, la variation 
V de la vitesse pour un accroissement (ou un pas) t=0.010s
voila en vous remerciant
1] Pour le bilan des forces, je suppose que tu t'en es sorti, poids et frottements.
Ensuite pour trouver l'équation différentielle du mouvement, pense à utiliser la 2ème loi de Newton.
à minisep
pour le bilan des forces j'ai la poussée d'archimède le poids ainsi que la force de frottement ensuite pour l'équation différentielle j'ai trouvé:
g(1-(
fluide/objet))=(k/m)+(dV/dt)
mais je sais si c'est ça 
a oui je l'avais oublier 
g(1-(fluide/objet))=(k/m)V²+(dV/dt)
et après je sais pas comment démarrer
si t'as une idée tu peux m'en faire part merci
Utiliser la méthode d'Euler me semble être la meilleure solution.
Tu as dv/dt = a, l'accélération.
À la date tn, an = g(1-(fluide/objet)) - (k/m)vn².
En considérant que l'accélération a varie peut durant la durée t, utilise la méthode d'Euler pour trouver une relation entre vn+1 et vn.
1)
Poids de la bille (verticale vert de bas)
Poussée d'Archimède de l'eau sur la bille (verticale vers le haut)
Force de frottement eau-bille (vertical vers le haut).
(4/3)Pi.r³*2500*g - (4/3)Pi.r³*1000*g - kv² = (4/3)Pi.r³*2500.dv/dt
(4/3)Pi.r³*1500*g - kv² = (4/3)Pi.r³*2500.dv/dt
(4/3)Pi.0,008³*1500*g - 0,045v² = (4/3)Pi.0,008³*2500.dv/dt
0,0322 - 0,045v² = 0,0054 dv/dt
dv/dt + 8,33 v² = 6
-----
2)
Delta V = (6 - 8,33v²) * 0,01
Delta V = 0,06 - 0,00833v²
-----
Sauf distraction.
à J-P
je sais pas si c'est moi qui fait une erreur mais ici tu trouves ce résultat:
Delta V = 0,06 - 0,00833v²
moi je trouve:
Delta V = 0,06 - 0,0833v²
8.33*0.01=0.0833 et pas 0.00833
voila c'est tout
pour le reste merci
et maintenent je dois trouver une relation entre Vn à l'instant t[/sub]n =t[sub]n+1 +t et la vitesse Vn-1 a l'instant t[sub][/sub]n-1
merci
V(n+1) = V(n) + Delta V
V(n+1) = V(n) + (0,06 - 0,0833*(V(n))²)
V(n+1) = - 0,0833*(V(n))² + V(n) + 0,06
Avec Delta t = 0,01 s et V(0) = 0
-----
Sauf distraction.
ok merci J-P je comprend mieux l'exercice
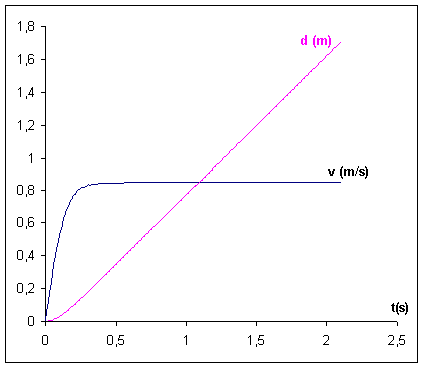
mais je vois pas comment je pourrais la représenter graphiquement V(t)
Sur le graphe, tu places le temps t en abscisse et la vitesse en ordonnée. Ensuite, en considérant la vitesse initiale nulle, tu peux trouver la vitesse après 0,01 s grâce à la relation entre vn+1 et vn. En effet, si v0 = 0 m.s-1, alors v1 = 0,06 m.s-1. Et ainsi de suite. Sur ton graphe, tu auras un point tous les 0,01 s.
Tu peux aussi trouver la vitesse limite à l'aide de l'équation différentielle 
Annuler
connectez vous