Inscription / Connexion Nouveau Sujet
Physique devoir maison terminale S
Bonjour,
J'ai besoin d'aide pour la question 2 d'un sujet pour mon devoir maison.
Énoncé : Stan plongé verticalement sans vitesse initiale d'une hauteur H = 28 m.
1.dans un premier temps la chute est considéré comme verticale sans vitesse initiale en détaillant le raisonnement vérifier que la durée de chute et voisine de 3 secondes et que sa vitesse d'entrée dans l'eau et proche de 90 kilomètres par heure (fait)
on considère maintenant que Stan se donne au moment du saut une vitesse initiale horizontale V0 = 2,0 mètres par seconde
2. déterminer à nouveau sa durée de chute est la norme sa vitesse d'entrée dans l'eau.
Je bloque à celle-ci je suppose qu'il faut calculer les coordonnées du vecteur vitesse avec la nouvelle condition initiale . Puis les coordonnées du vecteur position et donc en déduire avec la même formule que la question une la durée et la vitesse
Bonjour,
Je suppose qu'on est dans le cas d'une chute libre verticale ?
Si oui, une fiche sur le sujet : ![]() Mouvement dans un champ de pesanteur : chute libre verticale
Mouvement dans un champ de pesanteur : chute libre verticale
OK pour la première question.
Pour la deuxième, c'est exactement le même raisonnement en prenant une condition initiale différente de "0" dans tes équations paramétriques :
* Exprimer les coordonnées du vecteur vitesse initiale
* Déduire les coordonnées du vecteur vitesse par intégration des coordonnées de l'accélération et prise en compte des conditions initiales
* Déduire les coordonnées du vecteur position par intégration des coordonnées de la vitesse
Bonjour papyhenky et bonjour gbm
On peut aussi remarquer que la chute verticale de Stan sera la même dans les deux cas puisque l'accélération, la vitesse initiale (nulle) et la position de départ sont les mêmes. Et résistance de l'air (apparemment négligée ici) identiques.
Dans ces conditions pas besoin de calculs pour montrer que la durée de la chute sera la même.
Confirmation expérimentale ici : ![]()
Pour le calcul des vitesses on peut aussi utiliser le théorème de l'énergie cinétique.
***Edit gbm : salut odbugt1, il est parfois bon de confirmer des évidences par le calcul  ***
***
Il ne précise pas quil se trouve dans une chute libre car il ny a pas demande de négligé les forces de frottement.. je ne sais pas si supposer suffit donc.
En calculant les coordonnes de v et du vecteur position (que j'appelle OA) je trouve que la durée en faisant
OA(x=0
y=1/2*g*t^2 + 2.0
Donc avec th(hauteur parcouru)
yth=1/2*g*th^2 + 2.0
Th= ((2*28)/10)+2
((2*28)/10)+2
Et donc apres pour trouver la vitesse d'entrée dans l'eau je fais : g×th
Ça vous semble correcte?
Merci de vos reponses
***Edit gbm : salut odbugt1, il est parfois bon de confirmer des évidences par le calcul ***
Certes !
Surtout que bien souvent, "l'évidence" ne saute aux yeux que lorsque le calcul est terminé.
Bien souvent, les énoncés sont incomplets.
C'est probablement le cas ici et tu es bien obligé de négliger la résistance de l'air car on ne te donne aucun renseignement à son sujet.
Le mouvement du plongeur est décrit par l'expression des vecteurs accélérations, vitesse et position.
Je prends un repère orthogonal Ox,Oy avec Oy orienté vers le haut.
Pour le plongeon vertical sans vitesse initiale de la première question ces vecteurs sont :
Pour le plongeon parabolique avec vitesse initiale de la 2e question :
avec V0=2,0 m/s et H=28m
Un grand merci cest ce que j'avais en soit trouvé. Oy est vers le bas * ducoup j'enlève le négatif à g.
Je suppose que ensuite j'applique la formule que j'avais trouvé :
Th= ((2*28)/10)+2
((2*28)/10)+2
Mais je trouve 2.8s , c'est impossible que la chute soit plus longue que celle sans vitesse initiale :/
Ta "formule" Th=((2*28)/10)+2 est fausse.
Comme indiqué précédemment le vecteur espace a pour coordonnées :
A la date t=th le plongeur entre dans l'eau donc y=0
donc
Ok cest la meme formule que pour la 1ere question mais on en fait quoi du x=V0t.
C'est la que je bloque enfait..
Le x=V0t te permet, si besoin est, de connaître l'abscisse du plongeur à la date t
Par exemple à la date t=th au moment d'entrer dans l'eau l'abscisse du plongeur est :
D'accord j'ai compris ahah merci énormément !
Vu qu'il a une vitesse initiale c'est que son saut est parabolique et donc il faudra calculer le x pour savoir où sur l'axe des abscisses il entre dans l'eau, et ensuite calculer la vitesse de la chute ? Grâce au x
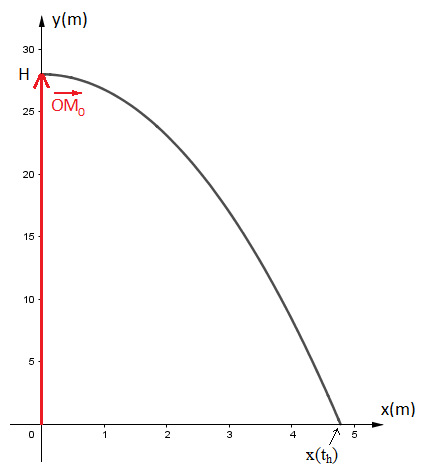
J'ai représenté ci-dessous le vecteur à la date t=0 pour le cas du mouvement parabolique, mais ce vecteur est le même pour le plongeon vertical.
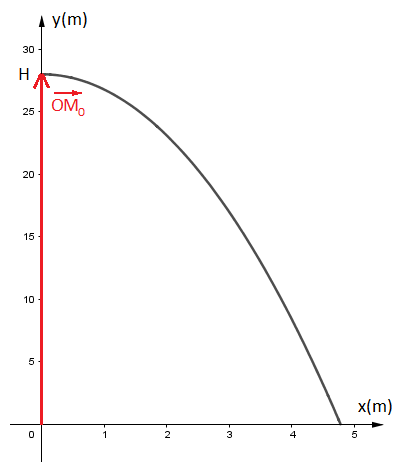
Bonjour,
merci de tes réponses. Je ne comprends toujours pas pourquoi si on calcule x(th) on obtient un résultat d'environ 5.2s. C'est 2 fois plus que la chute sans vitesse initiale. Maintenant que jy repense ca me semble normal car il a une trajectoire parabolique.
Et ca vitesse serait de 52m/s .. cest trop
Et si on utilise y(th) on obtient la même durée et la même vitesse que sans vitesse initiale.
Doit on melanger les 2 résultats ?
Je ne comprends toujours pas pourquoi si on calcule x(th) on obtient un résultat d'environ 5.2s.
Tu as bien raison de ne pas comprendre ! tu sembles confondre th qui est une date ( en s ) et x(th) qui est une abscisse (en m) alors ton x(th) = 5,2s est évidemment faux.
Tu n'as pas à te préoccuper de la valeur de x(th).
Je l'ai seulement évoqué à titre d'exemple pour répondre à ta question du 31-10-18 à 15:36
Pour calculer la vitesse d'entrée dans l'eau pour le plongeon parabolique deux méthodes sont possibles :
- Soit, comme indiqué dans mon post du 30-10-18 à 16:28, tu appliques le théorème de l'énergie cinétique. C'est la méthode la plus simple.
- Soit tu utilises, à la date t=th , les coordonnées du vecteur vitesse :