Inscription / Connexion Nouveau Sujet
période, pendule simple.
Bonjour, j'ai un exercice à faire mais je n'arrive pas à répondre à toutes les questions, pouvez-vous m'aider svp?
Doc 1:« J'ai pris deux boules, l'une de plomb et l'autre de liège, celle-là au moins cent fois plus lourde que celle-ci, puis j'ai attaché chacune d'elles à deux fils très fins, longs tous les deux de quatre coudées ; les écartant alors de la position perpendiculaire, je les lâchais en même temps ; une bonne centaine d'allées et venues, accomplies par les boules elles-mêmes, m'ont clairement montré qu'entre la période du corps pesant et celle du corps léger, la coïncidence est telle que sur mille vibrations comme sur cent, le premier n'acquiert sur le second aucune avance, fût-ce la plus minime, mais que tous les deux ont un rythme de mouvement rigoureusement identique.
On observe également l'action du milieu qui, en gênant le mouvement, ralentit bien davantage les vibrations du liège que celles du plomb, sans toutefois modifier leur fréquence.
Données :
Une coudée = 0,573 m Accélération de la pesanteur : g = 9,81 m.s-2
La masse du pendule de plomb de Galilée est : m = 50 g
Doc 2: On reproduit l'expérience de Galilée en laboratoire avec un pendule composé d'une bille de plomb de masse m = 50 g de centre d'inertie G, et d'un fil de longueur L accroché en O. On choisit la position à l'équilibre G0 de G comme origine des altitudes z. Pour un amortissement faible, la pseudo-période T du pendule est voisine de sa période propre T0. L'expression de la période propre est T= 2
 (L/g)
(L/g)
Doc 3: Je n'arrive pas à ajouter le graphique mais il représente l'évolution de l'abscisse x du centre d'inertie G du système en fonction du temps.
xmax vaut 400 mm et xmin= -400 mm. Il s'agit d'oscillations sinusoïdales avec T= 3,1 s. Les oscillations sont toutes les mêmes.
x diminue et augmente au cours du temps.
1) En utilisant l'enregistrement du doc 3, déterminer:
- la longueur L du pendule du laboratoire.
J'ai trouvé: L = 2,38 m.
- l'angle initial que faisait le fil au moment ou la bille de plomb a été lachée
Je ne sais pas comment le trouver.
2) On suppose que l'altitude initial de la bille de plomb dans le laboratoire est zA= 5,0 cm. Calculer l'énergie mécanique de la bille au point A, point ou elle est lachée sans vitesse initiale.
J'ai trouvé Em= 2,4*10^2 J
3) Pourquoi peut on considérer, à la vue du doc 3, que l'énergie mécanique du pendule se conserve?
En déduire la vitesse v de la bille au point G.
4) Calculer:
- le travail du poids de la bille sur le déplacement de A à B.
- le travail de la tension du fil sur le déplacement de A à G.
Voilà, merci..
Bonjour.
- la longueur L du pendule du laboratoire.
J'ai trouvé: L = 2,38 m.
 2.4 m.
2.4 m.
- l'angle initial que faisait le fil au moment ou la bille de plomb a été lachée
Je ne sais pas comment le trouver.
 i
i  9.6°.
9.6°.
Calculer l'énergie mécanique de la bille au point A, point ou elle est lachée sans vitesse initiale.
J'ai trouvé Em= 2,4*10^2 J
Pourquoi peut on considérer, à la vue du doc 3, que l'énergie mécanique du pendule se conserve?
En déduire la vitesse v de la bille au point G.
Utilisez la conservation de l'énergie mécanique entre Gi et G0.
Calculer:
- le travail du poids de la bille sur le déplacement de A à B.
- le travail de la tension du fil sur le déplacement de A à G.
A est confondu avec Gi, mais B est-il confondu avec G0 ?
Pour le travail du poids, je vous rappelle un résultat du cours de 1° :
Ca devrait faire des merveilles ici !
Pour le travail de la tension du fil, le travail élémentaire de
Que peut-on dire des directions de
Quelle conséquence cela entraîne-t-il pour
Que vaut alors le travail de
A vous la main !
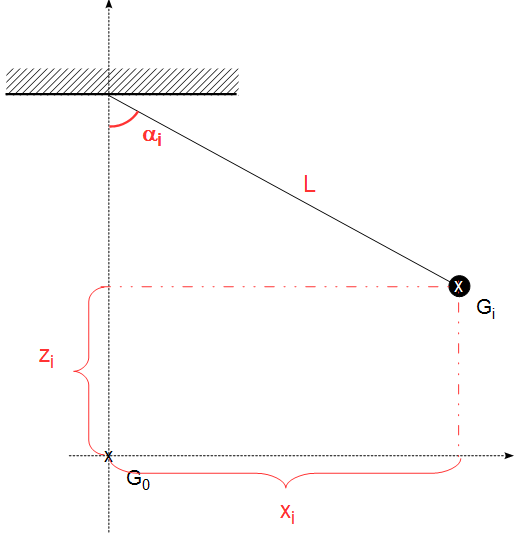
Merci beaucoup pour vos réponses!!
Pour l'angle initial, j'ai fait:
sin = xmax/ L = 0,4/4*0,573= 0,17 soit
= xmax/ L = 0,4/4*0,573= 0,17 soit  = 9,8°
= 9,8°
Pour l'énergie mécanique, j'ai refait le calcul et je trouve bien 2,4*10^-2 J
3) Il s'agit d'un régime peirodique: en l'absence de frottements, l'oscillation repasse périodiquement par sa position de repos avec une amplitude constante au cours de son mouvement. Les oscillations sont périodiques de période propre.
Les variations d'énergie potentielle et d'énergie cinétique se compensent. Il y a conservation de l'énergie mécanique.
S'il y avait des frottements, l'énergie mécanique diminuerait.
4) Pour la vitesse , je trouve environ 3,13 m/s.
Pour le travail du poids, j'ai fait:
W(P)= 50*10^-3*9,8*(2,292- 5,0*10^-2) 0,0245 J..
0,0245 J..
Pour le travail de la tension du fil, T et dl ont la même direction, vers le haut. Le travail T vaut donc 0?
Pour l'angle initial, j'ai fait:
sin
 = xmax/ L = 0,4/4*0,573
= xmax/ L = 0,4/4*0,573 S'il y avait des frottements, l'énergie mécanique diminuerait.
Les oscillations s'amortiraient et leur amplitude diminuerait.
4) Pour la vitesse , je trouve environ 3,13 m/s.
Pour le travail du poids, j'ai fait:
W(P)= 50*10^-3*9,8*(2,292- 5,0*10^-2)
 0,0245 J.
0,0245 J.Pour le travail de la tension du fil, T et dl ont la même direction, vers le haut.
4)  Em= 0
Em= 0
 Ec +
Ec +  Epp= 0
Epp= 0
Ecf - Eci + Eppf - Eppi= 0
1/2 m v² - 0 + 0 - m g h = 0
m g h= 1/2 m v²
g h = 1/2 v²
v²= 2 g h
v=  (2 g h)
(2 g h)
v =  (2* 9,8*2,4)
(2* 9,8*2,4)  6,9 m/s
6,9 m/s
Est ce correct?
Selon votre dessin, B est symétrique à Gi par rapport à l'axe des ordonnées.
En fait je ne sais pas à quoi correspondent zi et zf.
Merci !
4)
 Em= 0
Em= 0
Ec + Epp= 0
Ecf - Eci + Eppf - Eppi= 0
1/2 m v² - 0 + 0 - m g h = 0
m g h= 1/2 m v²
g h = 1/2 v²
v²= 2 g h
v= (2 g h)
v = (2* 9,8*2,4)
 6,9 m/s
6,9 m/s
Est ce correct?
D'après l'énoncé...
On suppose que l'altitude initiale de la bille de plomb dans le laboratoire est zA= 5,0 cm.
En fait je ne sais pas à quoi correspondent zi et zf.
Les altitudes se repèrent sur un axe vertical, orienté positivement vers le haut et dont l'origine est fixée, d'après l'énoncé, au point G0.
Doc 2...On choisit la position à l'équilibre G0 de G comme origine des altitudes z.
Selon votre dessin, B est symétrique à Gi par rapport à l'axe des ordonnées.
Pour la vitesse, je trouve 0, 99 m/s.
Merci beaucoup !



