Inscription / Connexion Nouveau Sujet
Pendule simple
Rebonjour à tous...
Une bille métallique est suspendue à l'extrémité d'un fil de masse négligeable de longueur L=50cm. L'autre extrémité du fil est fixée en un point O d'un axe vertical qu'un moteur peut faire tourner autour de son axe (pendule conique). Quelle l'angle en degré formé entre le fil et l'axe vertical lorsque celui-ci tourne sur lui-même avec une fréquence de 1 tour/seconde???
Merci d'avance à vous...
Re-bonjour.
Applique la seconde loi de Newton à la bille ; prends en compte le fait que le mouvement de cette bille est circulaire uniforme, ce qui impose certaines caractéristiques à son accélération ; déduis en une relation liant l'angle 
du fil avec la verticale, le rayon r du cercle décrit et l'accélération de la pesanteur g.
Exprime la relation trigonométrique liant , r et L.
Bidouille un peu ces deux expressions pour sortir .
A toi de jouer.
J'essaie de te suivre..
-P+Tcos(Téta)=-ma, T la tension du fil
Or selon la superposition des forces j'obtiens T=-P/cos(Téta)
Ce qui me donne : 2P=ma
2mg=ma
Donc 2g=a
On sait aussi que a=r(wcarré)
Donc r=2g/(2πN)carré
Et sin(Téta)=r/l
On a finalement: sin(Téta)=2g/[l(2πN)carré]
J'obtiens Téta=83°C c'est bien ça ??
Non, ça ne va pas dès la première ligne...
-P+Tcos(Téta)=-ma,
Quelles sont les caractéristiques du vecteur accélération ?
Aide toi d'un schéma (soigné !).
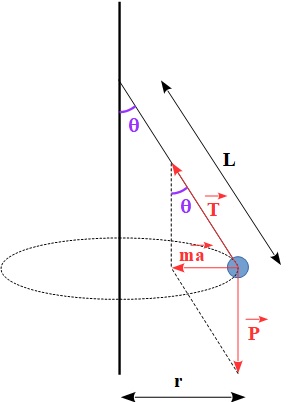
OK, vas-y...
Le titre de ton topic est "pendule simple", ici, il s'agit, comme tu le précises dans ton énoncé d'un pendule conique.
Attention !
Je viens de résoudre cet exercice, en fait j'orientais mal mon accélération, je travaillais plutôt avec l'accélération tangentielle.
J'ai fini par établir l'expression:
Cos=g/[l(2πN)[sup][/sup]]
Et de là j'ai trouvé=60°C. Vraiment génial merci picard.
j'ai trouvé
=60°C Le sup sup là en fait c'est "carré"
2.
Annuler
connectez vous