Inscription / Connexion Nouveau Sujet
Pendule pesant (disque homogène)
Bonjour, je reviens en pendule pesant. J'ai des problèmes avec le Théorème d'Huygens. Veuillez m'aider svp.
Problème
Un disque homogène de masse M, de rayon R, de centre d'inertie G peut osciller autour d'un axe ( ) horizontal perpendiculaire à son plan et passant par un point O de sa périphérie. Le disque est écarté de sa position d'équilibre d'un angle
) horizontal perpendiculaire à son plan et passant par un point O de sa périphérie. Le disque est écarté de sa position d'équilibre d'un angle  m faible puis lâché sans vitesse.
m faible puis lâché sans vitesse.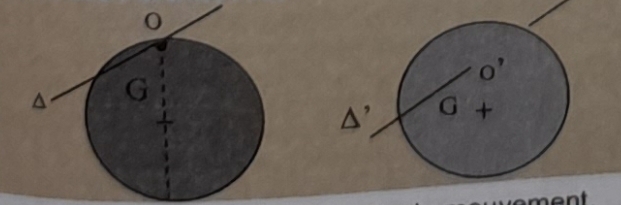 1)Établir l'équation différentielle du mouvement. Donner l'expression de la période T des oscillations. Calculer la période pour R = 20 cm ; g = 9,80 SI.
1)Établir l'équation différentielle du mouvement. Donner l'expression de la période T des oscillations. Calculer la période pour R = 20 cm ; g = 9,80 SI.
2) On fait maintenant osciller le disque autour d'un axe ( ') parallèle à (
') parallèle à ( ) et passant par O' situé sur le rayon OG, entre O et G tel que O'G = x.
) et passant par O' situé sur le rayon OG, entre O et G tel que O'G = x.
a) Donner l'expression de la période pour des oscillations d'amplitude faible.
b) Déterminer la valeur de x pour laquelle la période passe par sa valeur minimale.
c) Tracer la période T = f(x) pour
Bonjour
Le théorème de Huygens établit une relation entre le moment d'inertie par rapport à un axe  G passant par le centre d'inertie du solide et un axe
G passant par le centre d'inertie du solide et un axe  , parallèle à
, parallèle à  G et situé à la distance "d" de celui-ci. Si M désigne la masse du solide :
G et situé à la distance "d" de celui-ci. Si M désigne la masse du solide :
Ici, tu connais l'expression du moment d'inertie par rapport à  G, l'axe passant par G et perpendiculaire au plan du disque, donc...
G, l'axe passant par G et perpendiculaire au plan du disque, donc...
D'accord !
Maintenant commençons au début.
Question 1: Équation différentielle du mouvement
Par définition, l'énergie mécanique du système est : Em = Ec + Epp
• l'énergie cinétique est Ec = ½J
 ²
²
Avec J = JG + MR² (d'après le Théorème d'Huygens).
= JG + MR² (d'après le Théorème d'Huygens).
Mais JG = ½MR² pour un disque homogène mobile autour d'un axe passant par son centre.
Alors Ec = ½(½MR² + MR²). ²
²
Soit Ec = ¾MR². ²
²
• l'énergie potentielle de pesanteur du système est : Ep = - mgh (en prenant le niveau de référence le point O)
Mais h = R.sin m
m
C'est le bon chemin ?
Pour une position quelconque du pendule, l'élongation angulaire est  ,
,  m désignant l'amplitude angulaire.
m désignant l'amplitude angulaire.
Tu es bien sûr de ton sinus ?
Oh je vois !
h = R.sin
Alors Ep = - MgR.sin
L'énergie mécanique vaut alors :
Em = ¾MR². ² - MgR.sin
² - MgR.sin
Or Em = constante, donc sa dérivée par rapport au temps est nulle.
Donc 3/2MR² ".
". - MgR.
- MgR. 'cos
'cos = 0
= 0
Problème de trigonométrie concernant le sinus.
D'autre part, la dérivée par rapport au temps de ( ')2 est 2
')2 est 2 '.
'. ". Puisqu'il s'agit d'étudier un mouvement :
". Puisqu'il s'agit d'étudier un mouvement :  '
' 0 ; il est donc possible de diviser les deux termes de l'égalité par
0 ; il est donc possible de diviser les deux termes de l'égalité par  '.
'.
N'oublie pas que l'équation différentielle générale d'un mouvement d'oscillations sinusoïdales est de la forme générale :
 " +
" +  o2.
o2. = 0...
= 0...
Merci, je reprend.
h = R.cos
L'énergie mécanique vaut alors :
Em = ¾MR². ² - MgR.cos
² - MgR.cos
Je dérive : dEm = 3/2MR². ".
". ' + MgR.
' + MgR. '.sin
'.sin
Or  est trop petit, on peut écrire sin
est trop petit, on peut écrire sin


Ainsi dEm = 3/2MR². ".
". ' + MgR.
' + MgR. '.
'.
Alors dEm = 3/2MR². ".
". ' + MgR.
' + MgR. '.
'.
C'est ça ?
Juste une remarque : la dérivée de l'énergie mécanique se note :
.
En absence de frottement, l'énergie mécanique reste constante. Sa dérivée par rapport au temps est nulle à chaque instant.
La solution est une fonction sinusoïdale de la forme  =
=  mcos(
mcos( 0t +
0t +  )
)
En vérifiant que cette équation est bien la solution de L'équation différentielle précédente, on trouve la pulsation
Donc la période propre du mouvement est
AN : T0  1 s ; pendule battant la seconde
1 s ; pendule battant la seconde
2.a) Expression de la nouvelle période
• L'énergie mécanique du pendule est :
Em = Ec + Ep
• l'énergie cinétique est Ec = ½J '
' ²
²
• l'énergie potentielle est Ep = - Mgh
Mais h = x.cos
Donc Ep = - Mgx.cos
Alors l'énergie mécanique devient
Em = ½J '
' ² - Mgxcos
² - Mgxcos
Mais J ' = JG + Mx² (Théorème d'Huygens)
' = JG + Mx² (Théorème d'Huygens)
Avec JG = ½MR²
C'est bon, je peux continuer ?
J ' = ½MR² + Mx²
' = ½MR² + Mx²
Ainsi Em = ½(½MR² + Mx²). ² - Mgxcos
² - Mgxcos
dEm/(dt) = 0  (½MR²+Mx²).
(½MR²+Mx²). ".
". ' + Mgx.
' + Mgx. '
' = 0
= 0
En simplifiant par  ' on obtient
' on obtient
(½MR² + Mx²) " + Mgx.
" + Mgx. = 0
= 0
Du coup la période demandée est
A lire la question suivante, j'ai des doutes sur cette expression de la nouvelle période
Ton expression est correcte. Tu peux te rassurer en vérifiant que le cas particulier x=R conduit à l'expression de la période obtenue à la question précédente.
D'accord !
2.b) A présent, on demande la valeur de x pour laquelle T est minimal.
Là je n'ai pas compris. Pour moi, je devrais poser que tout ce qui est sous le radical  0 et résoudre pour répondre à la question. Mais cette expression sous le radical est déjà positive.
0 et résoudre pour répondre à la question. Mais cette expression sous le radical est déjà positive.
Tu as obtenue l'expression de T en fonction de x.Comme en math, il faut calculer la dérivée de T par rapport à x et remplir un rapide tableau de variations avant de tracer la courbe.
Remarque : la fonction "racine carrée" est monotone croissante. Les sens de variation de f(x) sont identiques à ceux de pour f(x)>0.
Tu n'as pas tenu compte de mon précédent message. Il suffit d'étudier les variations de :
mais ton résultat est correct. Tu viens de démontrer qu'il existe un extremum de T pour . Reste à montrer, en remplissant un tableau de variations comme en math, qu'il s'agit d'un minimum.
Oui, j'ai fait cela.
•  x
x  ]0 ; R/
]0 ; R/ 2 [, la fonction est strictement décroissante ;
2 [, la fonction est strictement décroissante ;
•  x
x  ]R/
]R/ 2 ; +
2 ; + [, la fonction est strictement croissante.
[, la fonction est strictement croissante.
Donc la valeur de x recherchée est
c) Maintenant on demande de tracer la fonction T = f(x)
Pour cela, est-ce que je dois calculer les limites de la fonction T(x) quand x tend vers 0 puis vers R ?
J'ai l'impression avoir un problème de maths 
C'est cela !
J'ai l'impression avoir un problème de maths
Pas tout à fait ! Il va falloir interpréter physiquement les deux limites trouvées !
Ces deux limites ont donné respectivement + et 1.
et 1.
Donc x = 0 est l'asymptote vertical
Avant de tracer, la courbe devrait suivre l'axe des ordonnées et descendre jusqu'à son minimum, ensuite remonter jusqu'à T = 1 s.
Pour cela je dois calculer aussi l'image de x = R/ 2
2
C'est ça ?
C'est cela ! Voici l'allure de la courbe, tracée pour R=1m. Il est assez difficile de bien visualiser à la fois le comportement asymptotique quand x 0 et l'existence d'un minimum en x= R/
0 et l'existence d'un minimum en x= R/ 2...
2...
N'oublie pas de justifier physiquement le comportement asymptotique .
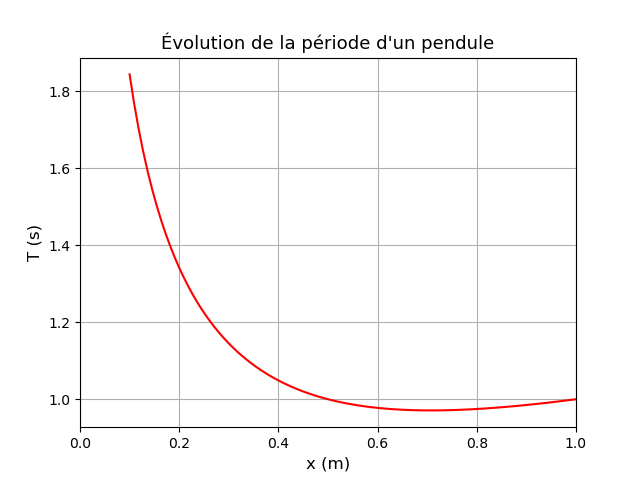
Ah là, la seule justification que je puisse dire est que la période décroît rapidement jusqu'à une certaine valeur, puis croit lentement vers la valeur limite.
Il est au repos.
Soit au repos soit animé d'un mouvement de rotation circulaire uniforme dans le cas général mais effectivement immobile s'il est abandonné sans vitesse initiale.


