Inscription / Connexion Nouveau Sujet
Pendule de Holweck
Bonjour tout le monde, veuillez m'assister ici svp.
Problème
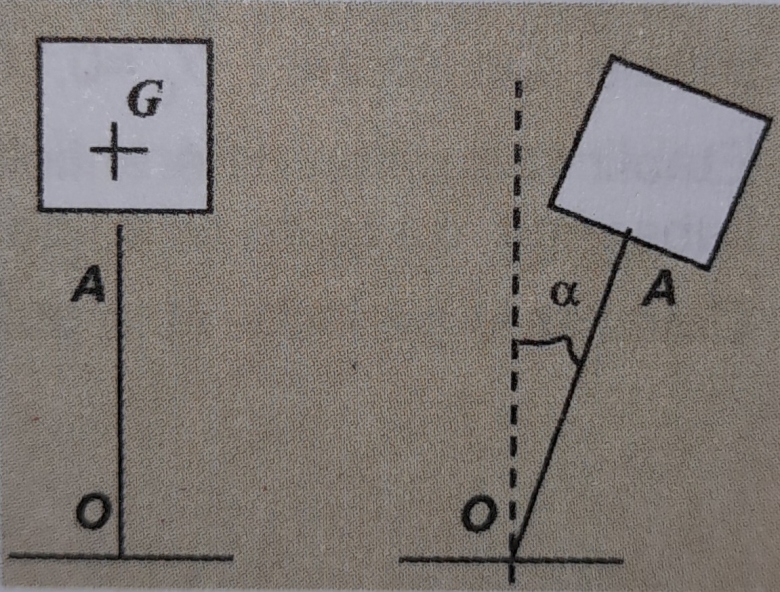
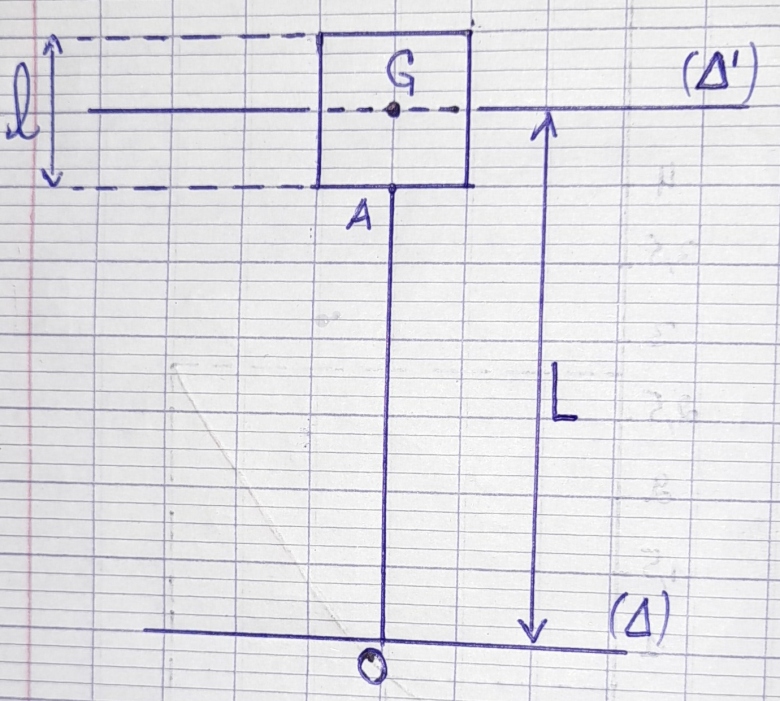
Une lame OA de masse négligeable est encastrée en O dans un support fixe et en A dans un cube plein et homogène en aluminium, d'arête l, le point A se trouvant au centre de la face inférieure du cube comme l'indique la figure ci-dessous. L'ensemble constitue le pendule de Holweck. On posera OG = l, G est le centre d'inertie du cube.
1) Sachant que le moment d'inertie du cube par rapport à un axe passant par son centre d'inertie G et perpendiculaire à deux faces, s'exprime par où M est la masse du cube et l son arête, en déduire le moment d'inertie du pendule de Holweck par rapport à un axe horizontal passant par O.
Application numérique : l = 2 cm ; L = 7 cm ;
masse volumique de l'aluminium 
= 2700 kg/m³.
2) On écarte le pendule d'un angle 
m par rapport à sa position verticale puis on l'abandonne.
On admet que la lame demeure rectiligne quand elle est inclinée et qu'elle exerce un couple de rappel dont le moment est proportionnel à l'angle d'inclinaison .
En notant C la constante de proportionnalité, écrire l'équation différentielle du mouvement.
3) Montrer que pour des oscillations de faible amplitude, le mouvement du pendule est sinusoïdal, à condition toutefois que la constante C soit supérieure à une valeur Co que l'on calculera. On donne g = 9,80 SI.
4) Calculer la période T des oscillations du pendule pour C = 0,0512 SI.
5) Que doit-il se passer quand C est égale ou inférieure à la valeur Co calculée au 3) ?
Bonjour,
Avec tout ce que tu as appris récemment sur les pendules, ca devrait aller très vite pour un tout petit exo comme ca 
D'accord, je vais tenter.
1) Moment d'inertie du pendule de Holweck
Soit (
O) un axe parallèle à 'G et passant par O. Le Théorème de Huygens donne :
• la masse volumique du cube est : = M/V 
M = .V = .l3
• J'G = JG = Ml²/6
En remplaçant M par son expression, J'obtiens :
J'G = l5/6
En remplaçant dans l'expression de JO, sachant que OG = L, J'obtiens enfin :
AN : je trouve
C'est ça ?
Oui ! J'ai repris le calcul, avec trois chiffres significatifs Jo = 1,07.10-4 kg.m2
2) Équation différentielle du mouvement
Le système est soumis à son poids et au couple de rappel dont le moment est
Le Théorème de l'accélération angulaire donne :
• or le poids rencontre l'axe de rotation O, donc son moment est nul.
Alors le Théorème de l'accélération angulaire devient :
- C = Jo" est l'équation différentielle du mouvement.
Si c'est bon, est-ce qu'à partir de l'expression de l'Em on peut aboutir au même résultat ?
• or le poids rencontre l'axe de rotation
O, donc son moment est nul.
Relis bien l'énoncé et regarde mieux le schéma fourni...
Si je comprend, le moment du poids est nul lorsque la lame est verticale (=0⁰).
Par contre, lors du mouvement autour du point O, le poids s'oppose. Son moment est alors :
= - P.d (d = OG.sin = L.sin)
Donc le moment du poids est = - PL.sin
Or
Or sin 
(faible amplitude) et P = Mg = .l3
Alors
Donc
Avant d'ecrire quoi que ce soit , il faut bien definir le parametrage (et en particulier les orientations).
On en avait pourtant deja longuement discuter une fois en ce qui concerne l'Epp .
Ici ce sont les moments qu'il faut bien traiter...
J'ai oublié le "g" dans l'expression du poids
En passant par l'énergie mécanique, j'ai trouvé la même chose.
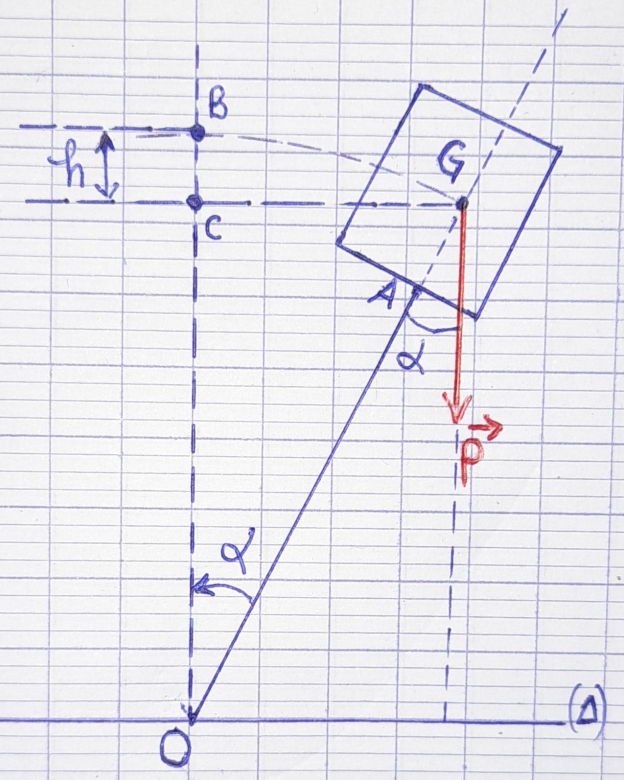
Voici mon schéma que j'ai utilisé
Bonjour, j'ai pensé au moment du couple de rappel. Ce couple tend à ramener le pendule à sa position d'équilibre, son moment doit être positif et est proportionnel à : c = C
Le poids s'oppose au mouvement, son moment est négatif = -P.L.sin
Maintenant, le théorème de l'accélération angulaire donne :
-PLsin + C = Jo"
Pour faible, sin
Donc -PL + C = Jo"
Or P = Mg = l3
Donc
Je ne sais pas si c'est bon cette fois-ci.
Ce qui me bloque réellement, je ne sais pas si le pendule tourne autour du point O ou s'il tourne autour de l'axe horizontal passant par le point O. J'ai posé cette question, c'est pour pouvoir traiter mes moments.
Bonjour,
Oui, c'est mieux mais il reste un souci avec le parametrage: si tu veux orienter dans le sens trigo, il est preferable de faire la figure avec >0 pour eviter les ennuis, or ici <0 sur ton dessin (si jai bien compris ton parametrage) : il faut ou refaire le dessin avec le pendule penché à gauche, ou changer l'orientation et garder ton dessin.
Le systeme tourne autour de passant par O et perpendiculaire au plan de la feuille. Donc ici, en representation plane (en coupe) , G tourne autour de O.
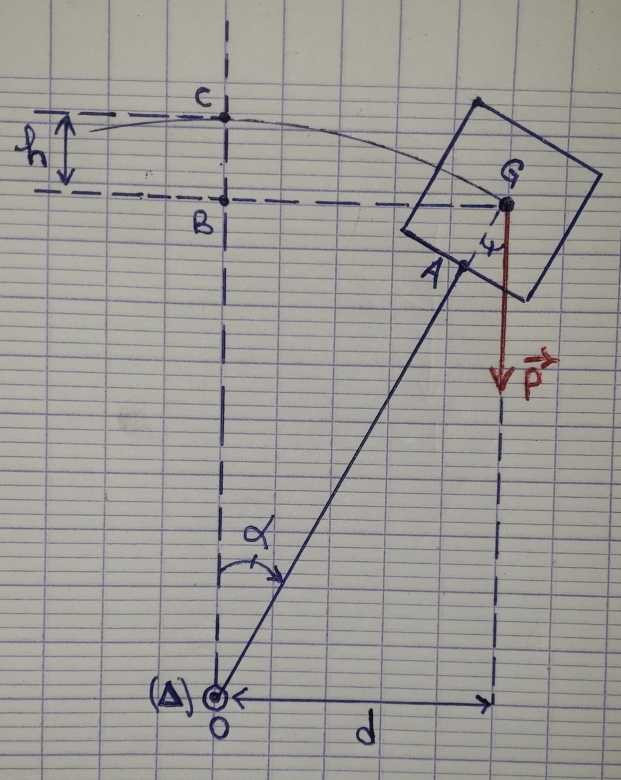
Voici mon nouveau schéma.
Selon la nouvelle orientation de , le moment du poids est positif et celui du couple de rappel négatif.
L'équation différentielle devient alors :
C'est ça ?
Merci.
Question 3)
Le mouvement du pendule est sinusoïdal si, dans l'équation différentielle, le coefficient de l'angle est positif. Ce qui revient à dire que
Donc
AN : Co = 0,0148176 = 1,48.10-2 SI
Co = 0,015 SI
Mais quelle est l'unité?
(Ecrire SI est un peu risqué car un correcteur un peu pointilleux peut croire que tu ne sais pas l'unité! )
AN : T = 0,34 s
J'ai utilisé les valeurs exactes et non les valeurs approchées, afin d'éviter des arrondis successifs.
On peut simplifier les expressions en remplacant MgL par Co
Jo" + (C-Co) = 0
si C > Co
Je trouve aussi T=0,34 s mais ca me parait bien rapide.
Question 5)
• si C = Co, on aura, dans l'équation différentielle " = 0
En intégrant successivement l'accélération angulaire, on trouve = 0. La lame est verticale.
• si C est inférieur à Co : là je n'ai pas d'idée
Question 5)
• si C = Co, on aura, dans l'équation différentielle
" = 0
En intégrant successivement l'accélération angulaire, on trouve
= 0. La lame est verticale.
Pas vraiment.
" = 0 => ' = cste
mais comme on lâche le pendule sans vitesse initiale,
' = ....
et donc
= ....
• si C est inférieur à Co : là je n'ai pas d'idée
Si C < Co ou encore C-Co < 0 je pense que la seule chose que tu puisses dire en Terminale est que le système n'oscille pas de part et d'autre de la verticale, puisque l'équa. diff. n'est plus celle d'un oscillateur.
Merci.
Les intégrations successives tiennent compte des conditions initiales.
À t = 0, o' = 0 '=0
Alors = m sachant qu'à t = 0 0 = m (pendule penché à droite)
Annuler
connectez vous