Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau terminale
Partager :

Pendule

Posté par
hdiallo 29-09-23 à 04:18

Bonjour, aidez-moi svp
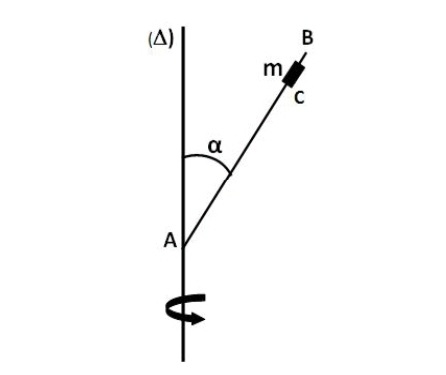
Problème : Une tige AB est soudée en A à un axe vertical (). Elle fait avec l'axe un angle α. Un petit anneau de masse m peut coulisser sans frottement sur la tige. L'ensemble tourne autour de l'axe avec une vitesse constante de N tours/s : l'anneau se fixe en un point C tel que AC = d. Pendule
1) Représenter les forces sur l'anneau.
2) Donner l'expression de d en fonction de N, α et g (intensité de pesanteur).
Exprimer la réaction de la tige sur la masse m.
AN : g = 10 SI ; α = 60° ; m = 10 g ; N = 2 tours/s.
3) On double la vitesse de rotation. Quelle doit être la valeur de l'angle α pour que l'anneau demeure à la même distance d du point A ?

Posté par
krinn Correcteurre : Pendule 29-09-23 à 10:40

Bonjour hdiallo,

ca faisait longtemps!
un problème facile pour toi.

où en es-tu ?

Posté par
vanoisere : Pendule 29-09-23 à 10:40

Bonjour
Le plus simple consiste à appliquer le principe fondamental de la dynamique dans le référentiel terrestre considéré comme galiléen. Peux-tu scanner ton schéma ?

Posté par
krinn Correcteurre : Pendule 29-09-23 à 10:41

bonjour vanoise, parfaitement synchone !!!

Posté par
vanoisere : Pendule 29-09-23 à 14:13

Bonjour krinn
Je te laisse bien volontiers gérer la suite.

Posté par
hdiallore : Pendule 29-09-23 à 17:25

1) Bilan des forces appliquées
- le poids \vec P = m\vec g de l'anneau ;
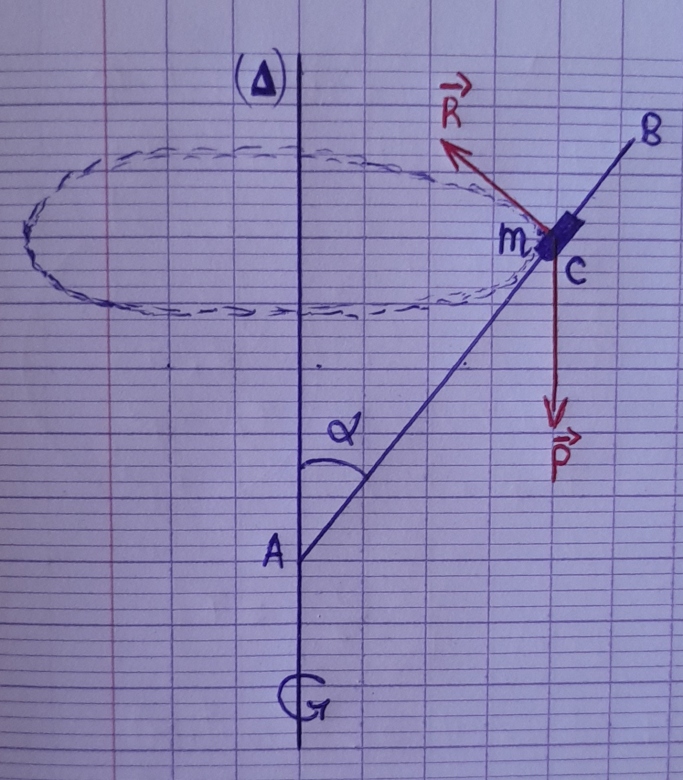
- la réaction \vec R de la tige AB sur l'anneau Pendule

2)Expression de d
J'applique le Théorème du centre d'inertie à l'anneau \sum{\vec F_{ext}} = m.\vec a

Donc \vec P + \vec R = m.\vec a

Or  \vec P + \vec R = \vec F_n (une force normale)

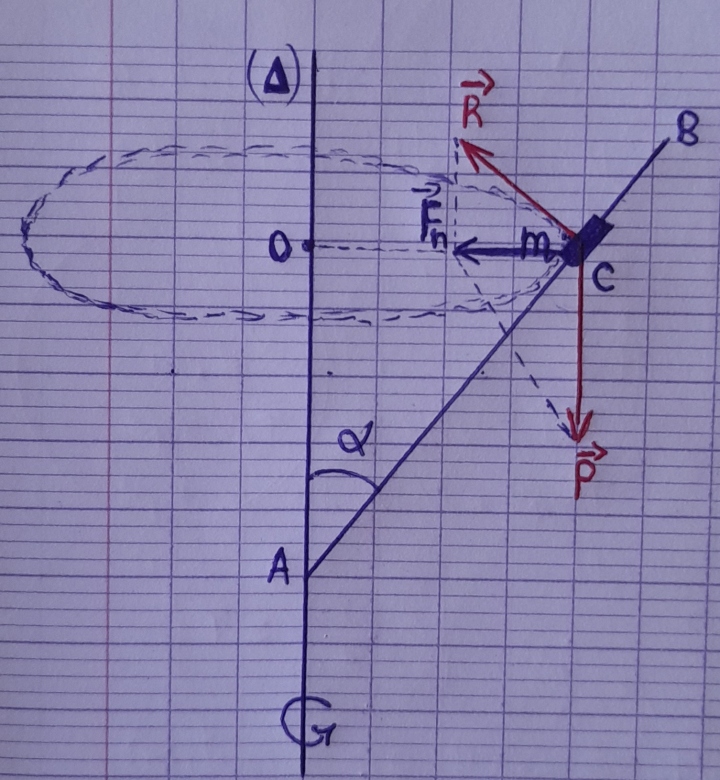
Suivant donc la normale, on a : Fn = mr² Pendule
Mon problème, c'est comment repérer l'angle entre ces vecteurs et exprimer Fn.

Posté par
krinn Correcteurre : Pendule 29-09-23 à 17:48

Citation :
Un petit anneau de masse m peut coulisser sans frottement sur la tige.


Donc \vec R est .... à AB et donc l'angle entre \vec R et la résultante vaut ....

Posté par
hdiallore : Pendule 29-09-23 à 18:45

\vec R est perpendiculaire à AB et (\vec F_n , \vec R)= \alpha

Dans ce cas : F_n = R.cos\alpha

• Le rayon r de la trajectoire est r = d.sin\alpha

• La vitesse angulaire est \omega² = 4\pi²N²

Or Fn = mr² (déjà établi)

Alors R.cos\alpha = m.d.sin\alpha. (4.\pi².N²)

Mon souci, g n'apparaît ici...lorsque je tire la distance d demandée

Posté par
krinn Correcteurre : Pendule 29-09-23 à 19:00

La 2e loi de Newton est vectorielle, elle donne, en général, plusieurs relations...

Posté par
hdiallore : Pendule 29-09-23 à 20:17

Ah d'accord !

Suivant la tangente : P - R = m.at

Or at = 0 car la vitesse est une constante.

Donc P = R R = mg

Alors  mg.cos\alpha = m.d.sin\alpha. (4.\pi².N²)

D'où d = \frac {g}{4\pi²N²}cotan\alpha

Posté par
krinn Correcteurre : Pendule 29-09-23 à 20:35

Suivant la tangente à la trajectoire on trouve : 0 = 0
( le plan (COA) est orthogonal à la tangente)

C'est pas faux, mais ça ne nous avance pas.

Posté par
hdiallore : Pendule 29-09-23 à 20:45

Alors là je suis bloqué...

Posté par
krinn Correcteurre : Pendule 29-09-23 à 21:07

Je ne vois pas ce qui te bloque:

tu as projeté le pfd sur (OC) et trouvé: R cos = m an

mais tu peux aussi le projeter sur un autre axe faisant intervenir R et P

Tu l'as déjà fait cent fois, non?

Posté par
hdiallore : Pendule 29-09-23 à 22:30

D'accord, sur l'autre axe, la tangente, on a :

-R.sin + P = 0 R.sin = mg  (2)

Sur la normale : R.cos = m.d.sin.(4².N²)   (1)

En faisant (1)/(2), on a : \frac {Rcos\alpha}{Rsin\alpha}=\frac {4\pi²N².m.d.sin\alpha}{mg}

Donc     d = \frac {g.cos\alpha}{4\pi²N².sin²\alpha}

Posté par
krinn Correcteurre : Pendule 29-09-23 à 22:38

Oui, mais ce n'est pas sur la tangente, c'est sur la verticale que tu projettes !
La tangente au cercle est normale au plan (COA) et donc aux forces.

Posté par
hdiallore : Pendule 29-09-23 à 22:56

D'accord !

Expression de R :
Sur la verticale : R.sin = mg

Donc R = \frac {mg}{sin\alpha}

AN : d = 4,2 cm  et  R = 0,115 N

Posté par
krinn Correcteurre : Pendule 29-09-23 à 23:16

Oui, 2 chiffres significatifs suffisent

Posté par
hdiallore : Pendule 29-09-23 à 23:38

R 0,12 N

3) Calculons la valeur de l'angle

Dans la relation (1) : R.cos = m.d.sin.('²)

Or ' = 2

Donc R.cos = m.d.sin.(16².N²)

D'où tan\alpha = \frac {R}{16\pi².m.N².d}

AN :  tan\alpha = 0,433 \Rightarrow \alpha = 23,4°

Posté par
krinn Correcteurre : Pendule 30-09-23 à 07:26

Attention, le sinus est au carré dans la formule donnant d

Posté par
hdiallore : Pendule 01-10-23 à 03:56

krinn, la RFD projetée sur l'axe horizontal ne fait pas apparaître le sinus au carré. Tu peux revoir mon message du 29-09-23 à 22:34

Posté par
krinn Correcteurre : Pendule 01-10-23 à 09:40

C'est vrai, mais dans le 3) la relation devient:

R' cos ' = .....

R dépend de , la valeur de R que tu as trouvée ne vaut que pour = 6O°

Posté par
hdiallore : Pendule 02-10-23 à 11:53

R'.cos' = m.d.sin'.(4².N²)
Ensuite R'sin' = mg

Avec ces deux relations, je peine à isoler l'angle ', car le sinus est au carré mais le cosinus non.

Posté par
krinn Correcteurre : Pendule 02-10-23 à 12:03

On part de :

d = \frac {g.cos\alpha}{4\pi²N².sin²\alpha}

Si on double la vitesse N, on a :

d' = \frac {g.cos\alpha'}{16\pi²N².sin²\alpha'}

Et on veut d' = d ce qui donne une équation vérifiée par '

Posté par
hdiallore : Pendule 02-10-23 à 12:19

Ah c'est moi qui n'ai pas pris en compte le fait que ' = 2

Ainsi R'.cos' = m.d.sin'.(16².N²)
Ensuite R'sin' = mg

En prenant rapport membre à membre de ces deux relations, j'obtiens


d = \frac {g.cos\alpha'}{16\pi²N².sin²\alpha'}

Ce qui est en accord avec ce que tu as trouvé.

Maintenant mon problème, c'est comment isoler l'angle '. Problème de trigonométrie sûrement

Posté par
krinn Correcteurre : Pendule 02-10-23 à 12:22

Oui, mais vraiment un tout petit....😀

Posté par
hdiallore : Pendule 02-10-23 à 12:39


d = \frac {g.cos\alpha'}{16\pi²N².sin²\alpha'}
\frac {sin²\alpha '}{cos\alpha '} = \frac {g}{16\pi²N².d}

Donc \frac {1 - cos²\alpha '}{cos\alpha '} = \frac {g}{16\pi²N².d}

{1 - cos²\alpha '}= \frac {g}{16\pi²N².d} cos\alpha '

J'obtiens un polynôme du second degré dont l'inconnu est cos'

Posté par
krinn Correcteurre : Pendule 02-10-23 à 13:01

Oui, et l'exo est fini.

Posté par
hdiallore : Pendule 06-10-23 à 02:32

AN :
26,5cos²' + 10cos' - 26,5 = 0

Je trouve = 2909 = 53,9

d'où les racines :

• cos'1 = -1,2056 (à rejeter)

• cos'2 = 0,828 ' = 34⁰

Posté par
krinn Correcteurre : Pendule 06-10-23 à 07:13

Oui, toutefois pour éviter les erreurs intermédiaires (26,5) il vaut mieux partir de:

d = \frac {g.cos\alpha}{4\pi²N².sin²\alpha}

d' = \frac {g.cos\alpha'}{16\pi²N².sin²\alpha'}

et écrire d'=d puis simplifier:

d'=d
<=> \frac {g.cos\alpha'}{16\pi²N².sin²\alpha'}= \frac {g.cos\alpha}{4\pi²N².sin²\alpha}

<=> \frac {cos\alpha'}{sin²\alpha'}= \frac {4.cos\alpha}{sin²\alpha} = 8/3

<=> cos\alpha' = \frac {8}{3} sin²\alpha'

<=> 8 cos²\alpha' + 3 cos\alpha' - 8 = 0

Posté par
hdiallore : Pendule 07-10-23 à 02:07

Merci bien krinn


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !