Inscription / Connexion Nouveau Sujet
oscillations mécaniques libres 5
Bonjour
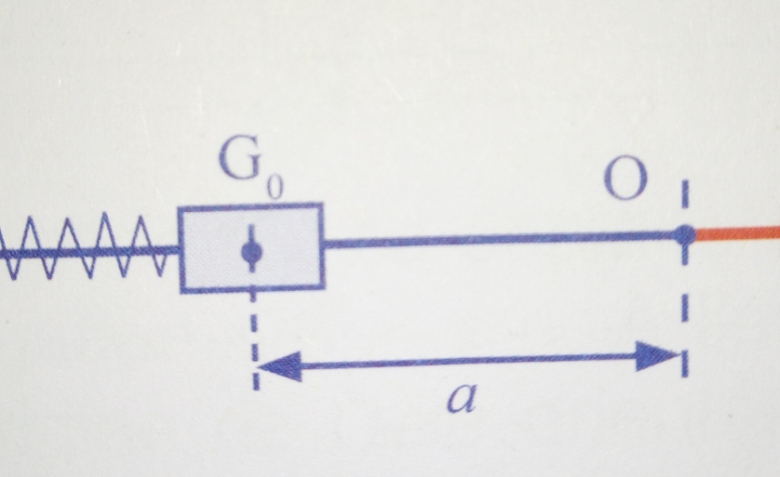
Lors d une séance de travaux pratiques , ton groupe étudié un oscillateur mécanique afin de représenter ses différents énergies .l oscillateur mécanique est constitué d un solide de masse m=200 g , d un ressort a spires non jointives de raideur k=26 N/m ,de masse négligeable . l ensemble peut glisser sans frottement le long d un axe(o,i) horizontal. Le solide est attaché a l une des extrémites etant fixé rigidement. Le système est raccourci a partir de sa position d équilibre ,d une longueur a=3 cm , et est lâché a t=0 s sans vitesse initiale.la référence des énergies potentielles de pesanteur est le niveau de l axe (o,i)
Tu es choisi pour la rédaction du compte rendu
1/ établis l équation horaires caractérisant le mouvement du centre d inertie du solide
2/ exprime
2/1 l énergie cinétique Ec du système
2/2 l énergie potentielle Ep du système (masse+ressort)
2/3 .l énergie mécanique Em du système (ressort +masse)
3) déterminer
3/1) la valeur maximale de la vitesse du solide
3/2 l accélération maximale du solide
4/ représente qualitativement les énergies Ec, Ep,Em
Réponse
Question 1
x=xm*cos(wot+ )
)
déterminons xm,  et wo
et wo
Wo=√(k/m)
wo=√{26/0,2)
wo=√130
wo=11,4 rad/s
x(0)=xm*cos =0
=0
 =-pi/2 et
=-pi/2 et  =pi/2
=pi/2
x"'(0)=[tex]-xm*w^2o*cos =-3
=-3
Je n arrive pas a continuer
Merci d avance
[/sub]
Re-hello
à t= 0,
et ou bien
selon le sens dans lequel tu décides d'orienter l'axe 0x ,
On considère souvent x>0 pour un allongement et x < 0 pour une compression, ce qui revient dans ton schéma; à orienter Ox de la gauche vers la droite
Donc
et
Donc
(on considérera nulle l'énergie potentielle de pesanteur, constante durant l'expérience)


Comment vous avez trouvé cette formule
Euh ... tu te souviens des exercices précédents (oscillations libres 1, 2, 3, 4)
Les conditions initiales (position ET vitesse) te permettent de déterminer xm et phi
A toi, allez!!
OK
x(0)=xm*cos )=-3
)=-3
x'(0)=-xm*wo*sin =0
=0
 =0 et
=0 et  =pi
=pi
Xm*cos(pi)=-3
-xm=-3
xm=3 cm
finalement xm=3 cm, wo=11,4 rad/s ,  =pi
=pi
x(t)=3*cos(11,4t+pi)
Euh ....
Tu écris "Ep=1/2*kx^2 " puis 2 lignes plus loin "Ep = 0" Il y a une grosse contradiction 
Donc
On avait par ailleurs
Avec
Donc
On retrouve bien la conservation attendue de l'énergie mécanique en absence de travail de forces non conservatives
La vitesse est la fonction sinusoïdale du temps
(il y avait une petite coquille plus haut)
donc
Pour trouver l'accélération ... on dérive la vitesse
donc
On a calculé phi il y bien longtemps avec l'analyse des conditions initiales
Tu as même établi par toi même ( ) phi = pi
) phi = pi
Donc
Donc
C'est bon? tu as retrouvé le fi...l ?
Cette fois ci tu ne m'as pas pris de court ... j'avais anticipé ta question. (Je me dis tout de même que tu pourrais essayer de chercher par toi moi puis proposer tes solutions)
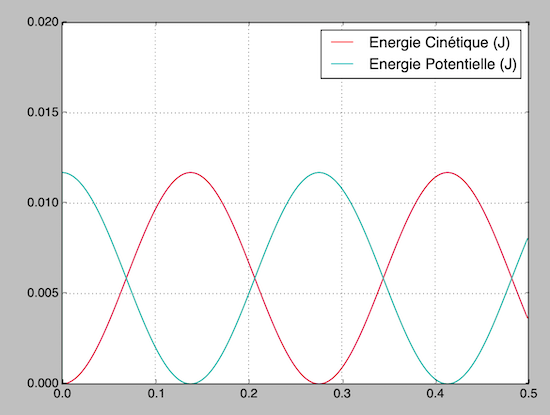
Ci dessous les représentation de l'Ec et l'Ep ce sont donc des fonction sinus2 et cosinus2
Peut être as tu une calculatrice avec fonctionnalités graphiques?
Alors maintenant, si tu veux me faire plaisir et surtout te faire progresser, comme tu disposes plus haut du corrigé:
Tu refais l'exonèrent tout seul, si tu cales tu regardes le corrigé et tu recommences
Et çe autant de fois que nécessaire jusqu'à faire l'exo de bout en bout par toi même.
(conseil d'anc^tre, mais promis ça marche plutôt bien)



