Inscription / Connexion Nouveau Sujet
oscillations mécaniques libres
Bonsoir
Énoncé :
On donne k=80 N/m, m1=100 g , H=2 m, g=10 m/s^2
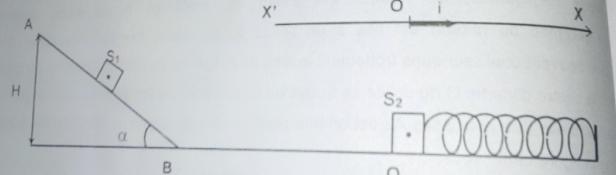
On réalisé un pendule élastique a l aide d un ressort hélicoïdal a spires non jointives de raideur k et d un solide S2 de masse m2 que supporte l extrémité libre du ressort
On dispose d une partie ABOC inscrit dans un plan vertical.
La partie AB est un plan incliné d un angle a par rapport a l horizontal de hauteur H.
La partie BOC est un plan horizontal .
On suppose que les pertes d énergies mécaniques en B sont négligeables .
Le pendule élastique est dans la position horizontal et le centre de gravité du solide est confondu avec le point O origine du repéré (O,i)
un solide S1 de masse m1=m2 est lâche du point A sans vitesse initiale.les frottements sont nuls sur toute la piste ABOC.
Les deux solides sont ponctuels..
1/ en prenant la référence de l énergie potentielle de pesanteur dans le plan horizontal contenant BOC ,calcule la vitesse du solide au point B en utilisant le principe de conservation de l énergie mécanique .
2/ montre que la vitesse du solide au point O est egale a sa vitesse au point B
3. Le solide S1 percute le solide S2,les deux solides restent solidaires après le choc.
3/1.montre que la vitesse de l ensemble { S1,S2} après le choc est V=3,16 m/s
3/2 en utilisant le principe de conservation de l énergie mécanique ,calcule le raccourcissement maximal subi par le ressort .
On précise qu a l instant du choc le ressort garde sa longueur a vide lo
3/3 montre que le système (S1,S2} est un oscillateur harmonique.
3/4 établis l équation horaire du mouvement .
On prendra pour instant initial, l instant du choc, et la position initiale ,la position correspondante
Question 1
Application de la conservation de k énergie mécanique
Em(A)=Em(B)
Ep(A)=EC(B)
m*g*H=1/2*m*V^2B
VB=√(2*g*H(
VB=√2*10*2
VB=√20
VB=6,32 m/s
Question 2
Application de la conservation de l énergie mécanique
Em(B)=Em(O)
1/2*m*V^2B=1/2*m*V^2O
VB=VO
VO=6,32 m/s
question 3/1
Bon , ici je ne sais pas quoi faire
Merci d avance pour votre aide
Salut.
A ce niveau, on applique la conservation de la quantité de mouvement c'est-à-dire la quantité de mouvement du système (s1 et s2 ) avant le choc est la même après le choc:
m1.v=(m1+m2).v' donc v'= (6,32 *0,1)/(0,1+0,1)=3,16m/s.


