Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau terminale
Partager :

oscillations mécaniques libres

Posté par
moussolony 08-01-20 à 12:40

Bonjour,

Enoncé :
Un ressort élastique de masse négligeable est fixé par une de ses extrémités. On suspend a l autre extrémité une masse M=500 g .
La constante de raideur du ressort est k=20N/m.

Questions :
1/ calculer l'allongement ao du ressort
2/ on écarté la masse M verticalement vers le haut de 5 cm a partir de la d'équilibre précédente prise pour origine des espaces et on  l'abandonne sans vitesse initiale.la masse se met a osciller verticalement .
2a/ montrer que le mouvement de M est rectiligne sinusoïdal
2b/ calculer la pulsation wo[u][/u] , la période To, la fréquence No, valeurs de l oscillateurs.
2-C/ donner la loi horaire du mouvement de M.sous forme x(t)=xm*sin(wot+).A t=0, M passe pour la 2eme fois en x=-2,5 cm
2d/ donner l expression de la vitesse v(t) de la masse m
2-e/ A quel instant M passe t elle pour la première fois par sa position d équilibre depuis t=0, et avec quelle vitesse ?
3/ en prenant la position d équilibre comme origine des energies potentielles de pesanteur ;
a/donner l expression de l énergie mécanique Em du système {masseM+ressort} en fonction de V, x, a0 et m, k
b/ montrer que cette énergie mécanique se conserve et calculer sa valeur.

Réponses

Question 1
J ai besoin d aide

Question 2a
J ai besoin d aide aussi

Question 2b
wo=(k/m)
wo=20/0,5)
wo=6,32 rad/s

To=(2pi)/(wo)
To=(2pi)/6,32.
To=0,32 s

No=1/(To)
No=1/0,32
No=3,125 Hz

Question 2c

x(t)=xm*sin(wot+)

D après les conditions initiales

x(0)=xm*sin()=-2,5
x'=xm*wo*cos()=0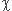
=-pi/2 ou =pi/2

Maintenant entre les deux angles lequel est la valeur exacte de .

Merci d avance pour votre aide

***Topic aéré : on ne va pas systématiquement passer sur tes sujets pour faciliter leur lecture => bonne résolution 2020 pour les prochains ?***

Posté par
diracre : oscillations mécaniques libres 08-01-20 à 13:44

Hello

Question 1:  peux tu citer les forces auxquelles est soumise la masse M

Tu écris alors la condition d'équilibre (somme des forces nulle) et tu trouves a0

Question 2c:  si xm fois sin(phi) = xm fois +1   combien vaut phi?

Posté par
moussolonyre : oscillations mécaniques libres 08-01-20 à 14:03

OK
Ces forces sont
Le poids P du solide
La tension du ressort T
La condition d équilibre
P+T=0
P=T
m*g=k*x
m*g=k(a-ao)
Mais on ne connait pas la valeur de a

Posté par
moussolonyre : oscillations mécaniques libres 08-01-20 à 14:08

Question 2c


=\frac{pi}{2}

Posté par
diracre : oscillations mécaniques libres 08-01-20 à 19:14

Citation :
m*g=k(a-ao)
Mais on ne connait pas la valeur de a


Quelle était la question posée?

Citation :
calculer l'allongement ao du ressort


a0 n'est pas la longueur du ressort ... c'est L'ALLONGEMENT initial du ressort (donc c'est "ton" a-a0)

Posté par
moussolonyre : oscillations mécaniques libres 08-01-20 à 20:51

Bonsoir
a-ao=m*g/k
a-ao=(0,5*10)/20
a-ao=0,25 m

Posté par
moussolonyre : oscillations mécaniques libres 08-01-20 à 23:01

Question 2a

Montrer que le mouvement de M est rectiligne sinusoïdal.

Posté par
moussolonyre : oscillations mécaniques libres 09-01-20 à 22:09

Bonsoir
Concernant la quest 2a
Est ce que je dois faire

Posté par
diracre : oscillations mécaniques libres 11-01-20 à 07:42

Je viens de relire ton post et de lire pour la première fois l'énoncé (ile faut toujours lire l'énoncé avec attention )

On avait donc a_0 = \frac{mg}{k}

Pour la suite, il faut munir l'espace d'un repère:
- l'origine t'est donné dans l'énoncé
- on choisit l'axe Ox (x "suggéré" par l'énoncé") comme étant l'axe vertical, disons orienté ... vers le haut (attention, on va en reparler)
- on choisit Oy et Oz arbtrairement dans le plan horizontal

2a/ l'énoncé te dit "la masse se met a osciller verticalement"
Tu as donc déjà l'information que le mouvement est rectiligne le long de l'axe Ox

Pour la démonstration de la propriété "sinusoïdale" je sèche (appel aux autres membres?) avec le bagage "Terminale". On me poserait la question dans la rue je répondrais:

a) RFD  fournit  \ddot{x} + \frac{k}{m}x =  0    

b) Equation différentielle du 2nd ordre dont l'ensemble des solutions un espace vectoriel de dimension 1 et qui contient le vecteur x(t) = cos(\sqrt{\frac{k}{m}}t)

mais je ne pense pas que cela soit la démonstration attendue

2b/ (pas fait le calcul numérique cependant)

2c/ ça devient plus raide (normal pour un ressort ...)

L'énoncé dit qu'à t = 0 la masse passe pour la 2ème fois en x0 = -2,5  cm
Et là patatras, le choix de l'orientation de la Ox a toute son importance, car selon son sens... on est pas du tout au même endroit dans l'espace à t = 0
Mais soit, NOUS avons choisi Ox vers le haut
Lorsqu'on lache la masse (t<0) elle ce trouve en x = +5 cm
De là elle descend vers le bas (t<0 toujours), passe par x=0 puis, toujours en descendant, une première fois par x0 = -2,5 cm (on a toujours t<0)
Puis atteint x= -5 cm où elle commence à remonter, et repasse par x0 = -2,5 cm
Et là on déclenche le chrono: t=0
Donc à t=0 la masse est en x0 et se déplace vers le haut  (dx/dt > 0)

Si on pose :  x = x_msin(\omega_0t + \varphi)

Tu as bien écris x(t=0) = x_msin\varphi = -2,5

Ensuite ça se gâte...

x_m est l'amplitude de la trajectoire sinusoïdale qui va de la position +5 cm à la position -5 cm, donc x_m = 5 cm

Donc sin\varphi = \frac{x_m}{x_0} = -\frac{1}{2}

Donc \varphi = -\frac{\pi}{6}   ou bien   \varphi = -\frac{5\pi}{6}

Pour trancher il faut s'intéresser à la vitesse

Tu as bien posé: \dot{x}(t) = +\omega_0x_mcos(\omega_0t+\varphi)

Et ce que l'on sait c'est que    \dot{x}(t=0) > 0     (la masse monte et Ox dirigé vers le haut)

Or \dot{x}(t=0) = +\omega_0x_mcos(\varphi)

Ce qui permet de retenir la valeur \varphi = -\frac{\pi}{6}

Tu as toutes les billes pour poursuivre je pense .... en espérant qu'il ne soit pas trop tard

Posté par
diracre : oscillations mécaniques libres 11-01-20 à 08:03

Citation :
Pour la démonstration de la propriété "sinusoïdale" je sèche  (appel aux autres membres?) avec le bagage "Terminale". On me poserait la question dans la rue  je répondrais:

a) RFD  fournit  \ddot{x} + \frac{k}{m}x =  0    

b) Equation différentielle du 2nd ordre dont l'ensemble des solutions un espace vectoriel de dimension 1 et qui contient le vecteur x(t) = cos(\sqrt{\frac{k}{m}}t)

mais je ne pense pas que cela soit la démonstration attendue  


Et en plus je dis des âneries ce matin. Mais bon on aura compris,  EV de dimension 2, de base sinus et cosinus, l'ensemble de solution sont des fonctions sinusoïdales du temps.

Café, jogging, sieste

Posté par
moussolonyre : oscillations mécaniques libres 11-01-20 à 13:06

Bonjour
Question 2a
Comme la masse se met a osciller verticalement . d où le mouvement est rectiligne. Et son équation horaire est de la forme
x(t)=Xm*sin(wot+].
finalement le mouvement de M est rectiligne sinusoïdal

Question 2e
Lorsque t=0, M passe pour la première fois par. Sa position d équilibre
Sa vitesse est
V(t)=31,6cos(6,32t-pi/6)

Question 3a
Em=\frac{1}{2}*m*v^2(t)+\frac{1}{2}*k*ao
Comment trouver le x dans l expression

Posté par
diracre : oscillations mécaniques libres 11-01-20 à 15:20

Citation :
Et son équation horaire est de la forme
x(t)=Xm*sin(wot+phi)
finalement le mouvement de M est rectiligne sinusoïdal


Sauf que c'est à la question 2A que l'on te demande de montrer que le mouvement est sinusoïdal et que c'est seulement à question 2C qu'on te propose de mettre l'équation horaire sous la forme x(t)=Xm*sin(wot+phi)

Citation :
Lorsque t=0, M passe pour la première fois par. Sa position d équilibre


  l'énoncé dit:

Citation :
A t=0, M passe pour la 2eme fois en x=-2,5 cm


Je t'engage à relire ce que j'écrivais à 7:42 ce matin

3A/  l'énergie mécanique est la somme de:

- l'énergie cinétique Ec=\frac{1}{2}mv^2

- l'énergie potentielle élastique  Ep_e=\frac{1}{2}ka^2
où a est la valeur algébrique de l'allongement du ressort par rapport à sa longueur à vide, donc  a = a_0-x  (je te rappelle que x> 0 lorsque l'élastique que plus court que sa position d'équilibre)

- l'énergie potentielle de pesanteur, choisie nulle pour x = 0, donc  Ep_p = \frac{1}{2}mgx

A toi?

Posté par
moussolonyre : oscillations mécaniques libres 11-01-20 à 20:36

Em=\frac{1}{2}*m*V^2+\frac{1}{2}*k*(ao-x)^2

Posté par
moussolonyre : oscillations mécaniques libres 11-01-20 à 20:43

Bonsoir
Pour la démonstration de la propriété sinusoïdale.
Je ne sais pas comment justifier cela

Posté par
gbm Webmasterre : oscillations mécaniques libres 11-01-20 à 20:55

Bonsoir dirac, moussolony,

Si les programmes de terminale n'ont pas trop changé ces dernières années, il me semble qu'il faut admettre la forme de la solution de l'équation différentielle (cf. ton cours) : x(t) = ...

Tu peux te référer à cette fiche du site également : Systèmes oscillants

Ensuite, ayant abouti par la deuxième loi de Newton à l'équation différentielle que tu as rappelée : \ddot{x} + \dfrac{k}{m}x = 0

il suffit de calculer \ddot{x}(t) = ...

et de remplacer x(t) et \ddot{x}(t) dans l'équation différentielle, pour aboutir à un résultat égal à 0.

Cela "démontre" que c'est bien une solution de l'équation différentielle (qui est de la forme sinusoïdale ...)

Posté par
moussolonyre : oscillations mécaniques libres 11-01-20 à 22:02

OK
x(t)=xm*cos(wot+)
x'=-xm*sin(wot+)
x''=x
+)
x

Posté par
moussolonyre : oscillations mécaniques libres 11-01-20 à 22:07

x+)
x

Posté par
moussolonyre : oscillations mécaniques libres 11-01-20 à 22:09

x

Posté par
moussolonyre : oscillations mécaniques libres 11-01-20 à 22:13

x"=-xm*w^2O*cos(wot+)
x"+w^20*x=0

Posté par
moussolonyre : oscillations mécaniques libres 11-01-20 à 22:16

Comme l équation differentielle est de la forme sinusoïdale. D ou le Mouvement de M est rectiligne sinusoïdal
C est ça?

Posté par
diracre : oscillations mécaniques libres 11-01-20 à 23:06

@moussolony

Juste pour mettre au propre:

x(t) = x_msin(\omega_0t+\varphi)

\dot{x}(t) = x_m\omega_0cos(\omega_0t+\varphi)

\ddot{x}(t) = -x_m\omega_0^2sin(\omega_0t+\varphi)

Donc \ddot{x}(t) = -\omega_0^2x(t)

@gbm
L'énoncé me semble quand même "boarderline"

Posté par
moussolonyre : oscillations mécaniques libres 11-01-20 à 23:15

finalement
Comme l équation différentielle est sous forme sinusoïdal. Donc le mouvement de M est rectiligne sinusoïdal

Posté par
diracre : oscillations mécaniques libres 11-01-20 à 23:32

Citation :
Comme l équation différentielle est sous forme sinusoïdal


Comme évoqué ce matin par mon je suis un peu désarmé sur ce genre d'énoncé et je vais laisser gbm (ou tout autre) conclure bien mieux que moi.

L'équation en elle même n'est pas "sinusoidale"
La loi horaire proposée en 2C est bien solution de l'équation différentielle
Mais en 2A, je ne vois pas comment prouver que la fonction est NECESSAIREMENT sinusoïdale sans le recours à l'artillerie mathématique hors programme du lycée.

Comme évoqué, je laisse la parole aux autres sachants. Et je serai aussi curieux de connaitre le corrigé qui te sera peut être proposé en cours

Posté par
moussolonyre : oscillations mécaniques libres 12-01-20 à 09:55

Question 2e
J aimerais savoir s il y a un calculer a faire pour déterminer l instant

Posté par
gbm Webmasterre : oscillations mécaniques libres 12-01-20 à 10:04

Effectivement dirac, cet énoncé est étrange parce que si on applique la méthode que j'ai proposée, on démontre bien que c'est une solution de l'équation différentielle .

Regarder cette vidéo, en particulier la deuxième partie ce celle-ci (solution de l'équation différentielle étant celle proposée par l'exercice de moussolony) :


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !