Inscription / Connexion Nouveau Sujet
oscillations mécaniques libres 2
Bonjour
Lors d une séance de TP, ton groupe étudié les oscillations mécaniques libres d un pendule horizontal afin de représenter son équation horaire .
Le pendule est constitué d un solide de masse m=0,1 kg, de centre d inertie G, attaché a l extrémité libre d un ressort horizontal, de raideur k.Il a un mouvement rectiligne sinusoïdal.au cours de ce mouvement ,le solide passe a la position initiale XO=0 m, avec une vitesse de valeur VO=0,5 m/s ,orienté vers l extrémité fixe.
Données :wo=7,85 rad/s, pi=3,14 rad
échelle :1,5 cm=> 1 cm, et 1 cm=> 0,2 s
Tu est choisi pour la rédaction du compte rendu
1/ établis l équation différentielle du mouvement du centre d inertie G du solide.
2/ montrer que l équation horaire x=Xm*cos(wot+ ) est la solution de l équation différentielle avec
) est la solution de l équation différentielle avec
4/ déterminé;
3/1 .To, ,Xm, et K
,Xm, et K
3/2 l équation horaire du mouvement du centre d inertie du solide
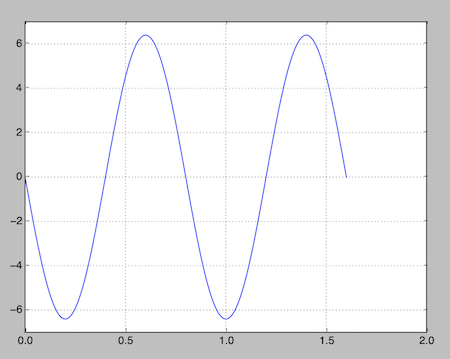
4/ représente sur deux périodes l équation horaire du mouvement
Réponse
Question
Système : le solide
Référentiel : terrestre suppose galiléen dans le repéré(0,i)
Inventaire des forces
Le poids P du solide
La réaction normale
La tension T du ressort.
Application du théorème du centre d inertie
P+Rn+T=ma
Projection dans le repéré choisi
-T=max
-T=mx"
-kx-mx"=0
Question 2
x=xm*cos(wot+ )
)
x'=-wo*xm*cos(wot+ )
)
*xm*cos(wot+
 ) et x" + (k*x)/m
) et x" + (k*x)/m
*cos(wot+
 )+ k*x/m=0
)+ k*x/m=0
-k/m*xm*cos(wot+ )=-kx/m
)=-kx/m
x=xm*cos(wot+ )
)
Question 3
An=> k=(7,85)^2*0,1=61,2 N/m
To=2pi√(k/m)
To=2*3,14*√(6,2/0,1)
To=49,6 s
x(t)=xm*cos(wot+ )
)
x'(0)=xm*cos =0
=0
Cos 0
0
 =-pi/2 ou
=-pi/2 ou  =pi/2
=pi/2
x'(0)=-wo*xm*sin(wot+ )=0,5>0
)=0,5>0
-wo*xm*sin >0
>0
Comme wo*xm>0
-sin >0
>0
Sin <0
<0
Sin(-pi/2)=-1<0 ou sin (pi/2)=1>0
 =-pi/2
=-pi/2
-wo*xm*sin(-pi/2)=0,5
xm=0,5/wo=0,5/7,85
Xm=0,06 m
Question 3/2
x(t)=0,06*cos(7,85t-pi/2)
Question 4
J ai besoin d aide
To=
Hello
En style télégraphique
La dérivée de de cos, c'est -sin
Pour déterminer phi, tu dois t'intéresser aux conditions initiales, je lis x(t=O) = 0
Enfin pour la question 4, en abscisse le temps, en ordonnée l'élongation x(t) , entre t = 0 et t = 2T0
Il me semble que tu te prends les pieds dans le tapis à plusieurs endroits:
1/ équation différentielle ,
2 / si , alors
et
Donc si
3/
m et
en choisissant l'axe Ox orienté vers l'extrémité libre du ressort
Donc et
Donc et
Soit, exprimé en cm
Bonjour
Question2
Si x=xm*cos(wot+ )
)
x'=-xm*WO*sin(wot+ )
)
(wot+
 )
)
mx"+kx=m( )+kx
)+kx
Mais je ne vois pas kx dans la response 2 que vous avez posté

tu factorises ce qui peut l'être, ie
Et tu obtiens bien
Sauf pbm de reveil domincal trop matinal de ma part ...
Tu te trompes à nouveau
pour converser le bon signe il faut un + pi/2 et non pas un - pi/2
enfin je te rappelle que cos(x+pi/2) = -sin(x) et que cos(x-pi/2) = sin(x)
Bref, une petite dose de rigueur en plus te rendrait service? 
Dans ton sujet "oscillations mécaniques libres 3" tu pointes d'ailleurs sur le thème: ce sont les conditions initiales (position et vitesse) qui te permettent de trancher sur la phase à l'origine (0 ou pi, +pi/2 ou -pi/2, ...)
Avec de l'entrainement ça va rentrer 
S il vous plaît la valeur de xm
J essais de refaire j ai trouvé que
x=0,5/7,85
Xm=0,06 m
Est ce que je suis bloqué de consertir en cm .
J ai une question ceux ci
Xm=50/7,85=6,4 m/ s
Pourquoi vous avez utilisé 50m/s or dans l énoncé c est plutôt 0,5
Je ne comprends pas
Alors
L'énoncé te dit:
et tu as établis avec
donc
Soit tu conserves l'unité de mesure de l'énoncé (le mètre):
Soit tu "anticipes" que l'ordre de grandeur de l'allongement de la vitesse sera le centimètre et tu convertis la vitesse en cm/s
C'est plus clair?

 /2)]
/2)]
