Inscription / Connexion Nouveau Sujet
Oscillations libres d'un circuit RLC
Bonjour,
Je dois fini un Tp a la maison. Seulement je n'arrive pas a voir sur quoi partir pour les dernières questions.
J'ai fait les questions d'avant qui était a faire au fur et a mesure de tp, et 4 question en rapport avec comment oscillaient la bobine ou le condensateur l'un par rapport a l'autre.
Voici les suivantes :
Calculer a l'aide des graphes le pourcentage d'énergie perdue par le condensateur en 1 oscillation, en 2 oscillations.
Quel pourcentage d'énergie est perdue pendant le transfert d'énergie entre le condensateur et la bobine lors du premier échange, du deuxième échange.
Si on avait enlevé la résistance de 9 ohm, les oscillations auraient elles été amorties ?
Quel est le nom du montage que l'on pourrait insérer pour que les oscillations restent non amorties. Que doit on réaliser ?
Voila, si vous pouviez m'aider a démarrer. Je ne vois vraiment pas par ou partir.
Merci d'avance.
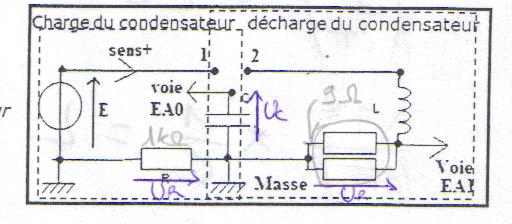
Bonsoir
Calculer a l'aide des graphes le pourcentage d'énergie perdue par le condensateur en 1 oscillation, en 2 oscillations.
Si je pense correctement, vous devriez avoir le graphe montrant l'évolution de uC(t).
De plus, vous savez que l'énergie emmagasinée par un condensateur, ici variable au cours du temps, vaut Ec(t) = (1/2)C.uC²(t)
Calculer Ec(t = 0), Ec(t = T) et Ec(t = 2T). Ainsi vous aurez votre perte d'énergie, à exprimer en %.
Procédez ainsi pour EL(t) = (1/2)L.i²(t) [je pense que vous devriez avoir également le graphe i=f(t) ].
Et de la même manière, vous avez Eélectrique
Eélect = EC + EL (décroissante)
Vous avez donc E(t = 0), E(t = T) et E(t = 2T) et donc les rapports à exprimer en %.
Le montage que vous recherchez s'appelle un montage à résistance négative (c'est le plus courant que l'on utilise en Tle mais ce n'est pas le seul possible)
Voir circuit ci-dessous. (Source :
)
R0 est variable, si on l'égalise à la valeur de la résistance du circuit (en l'occurence R+r ), il permet d'annuler la résistance totale du circuit et donc supprimer le "coefficient d'amortissement" rendant les oscillations libres non amorties !
Annuler
connectez vous