Inscription / Connexion Nouveau Sujet
oscillations forcées en régime sinusoidale
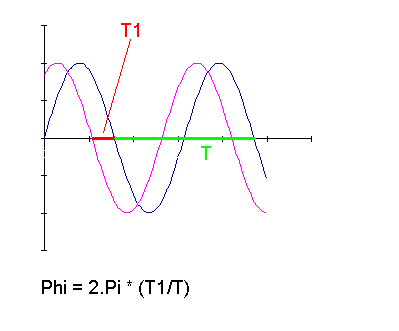
comment determiner graphiquement le déphasage entre deux courbes sinusoidales
Bonjour,
Je cherche une méthode qui permet, sans calcul, mais par une construction géométrique, de déterminer phi.
Pour déterminer le déphasage d'une sinusoïde, le début de la méthode est de construire un cercle trigo compris entre deux horizontales, tangentes du maximum et du minimum de la sinusoïde.
Il faut ensuite tracer une horizontale qui part du point d'intersection entre la sinusoide et l'axe des ordonnées (je crois). Cette horizontale coupe le cercle trigo en un point. Il suffit ensuite de mesurer l'angle avec un rapporteur.
Je cherche la description de la technique complète, notamment pour les angles allant de pi/2 à 2pi, je vous remercie d'avance.
Nath974,
Ce n'est pas un déphasage que tu cherches, mais plutôt la phase à l'origine (en t =0) d'une sinusoïde.
Il faut juste prendre garde, dans la construction de prendre le "bon" point d'intersection entre le cercle et l'horizontale qui part du point d'intersection entre la sinusoide et l'axe des ordonnées... Car il y a toujours 2 points et il faut choisir de bon (qui n'est pas le même en fonction de l'angle cherché).

Mille mercis pour la confirmation / eclaircissement et mille excuses pour la réponse tardive!
J'aurai une autre question:
A partir d'un spectre de raies (Amplitude en fonction de la fréquence) pour une onde complexe qui obéit a la serie de Fourier y(t) = A0 + A1sin(w1t+phi1) + A2sin(w2t+phi2) + ...
Y a-t-il un moyen de trouver la phase à l'origine (si j'ai bien compris) de chaque harmonique? On peut facilement lire l'amplitude A et retrouver la pulsation w (oméga) grâce à la fréquence, mais je ne trouve pas pour la phase...
Sachant que c'est pour une élève en école d'orthophonie et que le niveau en maths relève de la seconde (donc pas d'intégrales ou autres  )
)
Merci beaucoup