Inscription / Connexion Nouveau Sujet
Oscillations électriques forcées
Bonjour tout le monde, aidez-moi svp
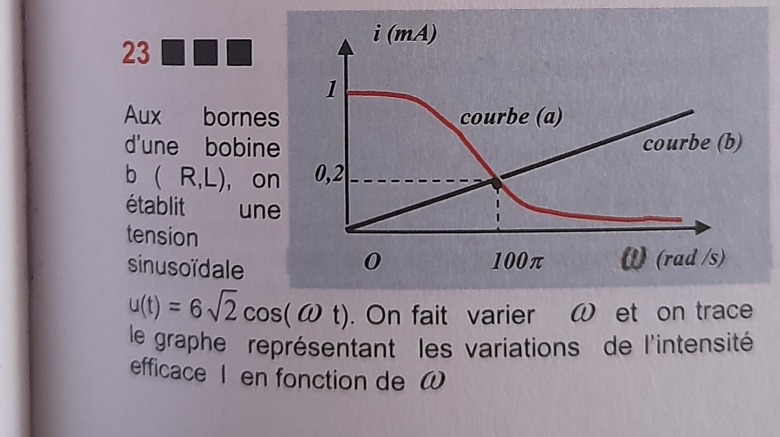
Problème : Aux bornes d'une bobine b(R,L), on établit une tension sinusoïdale . On fait varier ω et on trace le graphe représentant les variations de l'intensité efficace I en fonction de ω.
On remplace ensuite la bobine par un condensateur de capacité C. On fait de nouveau varier la pulsation ω et on trace le graphe qui traduit les variations de l'intensité efficace I en fonction de ω.
Les deux graphes sont donnés ci-dessous :
1) Identifier les courbes.
2) Déterminer les valeurs de R, L et C. 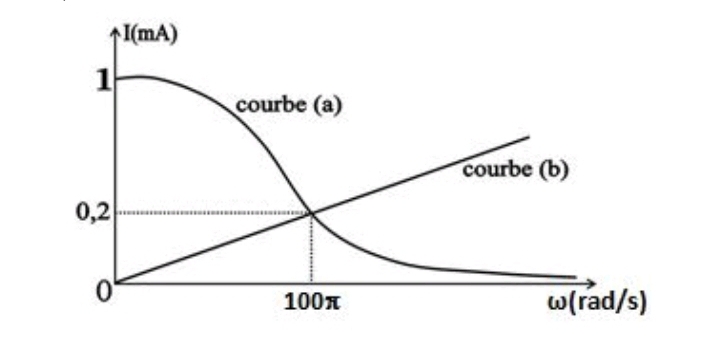
Bonjour
Il faut imaginer je pense la valeur efficace de la tension constante.
Écris les expressions des impédances des deux dipôles et tu pourras conclure.
1) Identification des courbes
• Aux bornes de la bobine : Ub = ZbI
Or
Donc
• Aux bornes du condensateur : UC = ZCI
Or
Donc
Conclusion :
La courbe (b) est celle du condensateur, car la fonction I = f( ) est l'équation d'une droite.
) est l'équation d'une droite.
Donc il ne reste plus que la courbe (a) qui est celle de la bobine.
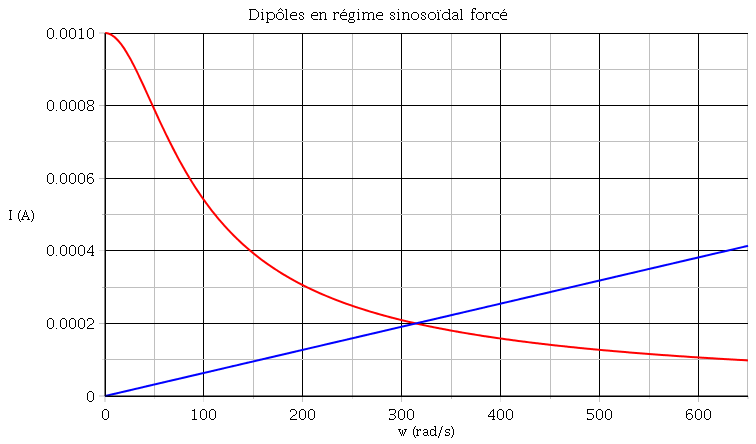
Petite mise au point : la courbe correspondant à l'intensité du courant à travers la bobine n'est pas tracée de façon rigoureuse. Elle laisse supposer l'existence d'un maximum de l'intensité efficace pour une pulsation voisine de 10 rad/s. Il n'en est rien : I est fonction monotonne décroissante de la pulsation et présente un maximum avec tangente horizontale en
rad/s. Il n'en est rien : I est fonction monotonne décroissante de la pulsation et présente un maximum avec tangente horizontale en  =0.
=0.
D'accord.
Question 2) :
À l'intersection des deux courbes, la pulsation est la même et l'intensité efficace aussi.
Donc j'égale les deux expressions de I, j'obtiens une 1ère relation.
Maintenant c'est la suite que j'ai pas compris. Normalement, puisqu'il y'a 3 inconnus, il me faut 3 équations
Il faut commencer par déterminer R car cela se fait "de tête" de façon immédiate en considérant le cas particulier  = 0.
= 0.
Ensuite, ta méthode conduit à la détermination de L et C.
D'accord.
Pour  = 0, I = 10-3 mA
= 0, I = 10-3 mA
Donc Zb = R = Ub/I
On retrouve la loi d'Ohm pour un conducteur ohmique pur.
Mais vanoise, la valeur de Ub n'est pas donnée pour procéder à l'application numérique de R
Énoncé incomplet. Impossible de résoudre sans connaître la valeur efficace U de la tension d'alimentation. J'ai choisi, un peu arbitrairement, U= 100mV pour tracer les courbes précédentes.
D'accord. Dans ce cas R = 100 
Toujours sur la courbe, pour I = 0,2 mA  = 100
= 100 rad/s ; aux bornes du condensateur, on a :
rad/s ; aux bornes du condensateur, on a :
I = UC
 C = I/(U.
C = I/(U. )
)
C  6,4
6,4  F
F
Je précise que c'est bien moi qui ai omi à la saisie l'expression de la tension sinusoïdale. Elle figure bien dans l'énoncé fourni par le document !
Du coup, la valeur de la tension efficace d'alimentation est U = 6 V
L'essentiel de l'exercice est compris ! Il suffit juste de transposer les expressions déjà établies, mais en remplaçant partout la valeur de la tension efficace par 6 V au lieu de 100 mV.
On trouve ceci :
R = 6000 
C = 106 nF
L = 93,6 H
À mon avis : juste une faute de frappe de la part de celui qui a fait le graphique car l'énoncé précise bien que l'axe des ordonnées correspond à la valeur efficace de l'intensité.


 2.cos(
2.cos(
