Inscription / Connexion Nouveau Sujet
oscillation électrique forcée
Salut, aidez moi pour cet exercice svp:
On considère trois dipôles associés en série : un conducteur ohmique de résistance R ,une bobine d'inductance L, et de résistance r, un condensateur de capacité C. ils sont branchés aux bornes d'un générateur délivrant une tension sinusoïdale. A l'aide d'un voltmètre, on a mesuré les tensions efficaces : UR=24V; UC=50V; U=30V, tension efficace aux bornes de l'ensemble. A l'aide d'un oscillographe, on a trouvé que la tension U aux bornes de l'ensemble est en retard de phase -30° par rapport à l'intensité.
1) Soit a la phase de la tension par rapport à l'intensité aux bornes de la bobine. représenter sur un diagramme de Fresnel les tensions UR, UB, UC et U. Faire apparaître sur le schéma a et b, sachant b=-30° phase de la tension par rapport à l'intensité.
2) Montrer que :
tan(a)= UC-Usin(b)/Ucos(b)-UR et UB= Ucos(b)-UR/cos(a).
Cordialement
***Edit gbm : bug sur le topic corrigé***
Bonjour,
Je suppose que dans la question 2 il faut lire :
(Ucos(b)-UR)/cos(a) à la place de Ucos(b)-UR/cos(a)
Merci de confirmer (s'il y a lieu )
Peut être pourrais tu proposer un diagramme de Fresnel ...
Une fois celui ci obtenu, la question 2 se traite par de la trigonométrie.
Pour ne pas travailler inutilement j'attends d'abord une réponse à ma demande formulée dans mon post du 23-03-19 à 09:59 au sujet de la question 2 :
Faut il lire :
comme tu l'as écrit
ou bien:
Diagramme de Fresnel :
Pour davantage de clarté, les tensions et les angles sont représentés sans tenir compte des échelles.
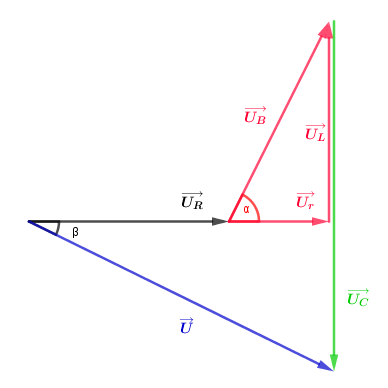
Merci beaucoup.
Mais dans le triangle où b est l'angle, comment on trouve le côté adjacent ? Moi j'ai trouvé UR+Ur.
cordialement.
il me semble en effet évident qu'il est égal à UR + UrJ'ai du mal à te suivre ...
Rappel de l'énoncé : L'angle α est le déphasage intensité tension aux bornes de la bobine.
L'angle β est le déphasage intensité tension aux bornes de l'ensemble R,L,C
On a tan(α) = UL / Ur (Voir le diagramme de Fresnel)
A partir de là on arrive facilement à :
tan(α) = ( UC - Usin(β) ) / ( Ucos(β) - UR )
Annuler
connectez vous