Salut, j'ai une question dans un exercice qui me pose problème...

En fait j'ai un circuit avec en série : une bobine L, deux résistances R1 et R2, un condensateur C, et un générateur de force électromotrice E.

L'équation différentielle du second ordre vérifiée par la tension u (aux bornes du condensateur) est :

d²u/dt² + (R1+R2)*u/L + u/(LC) = E/(LC)

On me dit : Dans le cas particulier où R1=R2=0 ohm, montrer que la tension aux bornes du condensateur évolue de manière sinusoïdale et exprimer la pulsation oméga₀ des oscillations en fonction des données.

Et là je bloque...


La nouvelle équa diff devient : d²u/dt² + u/(LC) = E/(LC)

Mais après ?

Merci d'avance pour votre aide

*** message déplacé ***

Désolé pour le multi-post, j'avais un doute sur le niveau de l'exercice et l'ai donc posté aux deux niveaux qui me semblaient être le plus en adéquation...

Salut,

d²u/dt² + u/(LC) = E/(LC)
se résout comme pour ton autre exo : somme d'une solution particulière et une solution homogène.

Ah oui, donc u(t) = E + Acos(wt) + Bsin(wt) et je détermine A et B c'est ça ?

OUI c'est ça

Ok merci beaucoup gbm !

Je t'en prie

Salut, j'ai déjà demandé de l'aide aujourd'hui pour des questions qui me posaient problème.

Ces questions font en fait partie d'un exercice qui est le suivant.

J'ai le circuit suivant :



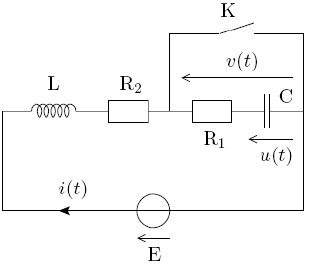
On me dit que "Initialement, l'interrupteur K est fermé depuis un temps suffisamment long pour qu'un régime continu soit établi. A la date t = 0, l'interrupteur K est alors ouvert. On note t = 0- la date qui précède immédiatement l'ouverture de l'interrupteur et t = 0+ la date qui la suit immédiatement".

1) Déterminer alors en justifiant la valeur des grandeurs électriques u, v et i à t = 0-, à t = 0+, puis à t = +oo

Donc pour cette question, j'ai :
pour t = 0- : u = 0 , v = 0 , i = E/R2
pour t = 0+ : u = 0 , v = E.R1/(R1+R2) , i = E/(R1+R2)
pour t = +oo : u = E , v = E , i = 0.

2) Etablir l'équation différentielle vérifiée par u.

J'ai trouvé finalement d²u/dt² + (R1+R2)u/L + u/(LC) = E/(LC)

3) Pour le cas où R1=R2=0 ohm, montrer que u oscille et déterminer sa pulsation propre.

La nouvelle équa diff : d²u/dt² + u/(LC) = E/(LC)
Donc u = E + A.cos(wt) + B.sin(wt)
Et là ça se corse : Conditions initiales : u(t=0+)=0=E + A.cos(0) + B.sin(0)
Donc A = -E Mais comment déterminer B ???


Merci d'avance, en espérant que j'aie juste aux questions précédentes.



*** message déplacé ***

Petite erreur au 2) : il faut lire d²u/dt² + (R1+R2)/L*(du/dt) + u/(LC) = E/(LC)

*** message déplacé ***

Concernant la première question, quelle est l'influence de la présence de la bobine sur la continuité du courant lors de l'ouverture de l'interrupteur?

*** message déplacé ***

Bonjour et joyeux noël ^^
j'ai à faire le même dm,
j'ai trouvé la même ED et j'en ai déduit que la pulsation valait ₀ = 1/LC

on a R1=R2=R donc d²u/dt²+ 2R/L du/dt + 1/LC u= E/LC

Q4: déterminer en fonction de L et de C la résistance R=R_cri pour laquelle u(t) évolue suivant un régime critique

R4: on veut = 0 et je trouve R=L/C

Q5: On pose pour la suite de l'exercice R=1/2 R_cri et ₀ = 1 rad/s
réécrire l'ED vérifiée par u et t>0

R5: j'ai remplacé par les données dans l'ED et j'ai d²u/dt + R_cri/L du/dt + u= E/LC
soit d²u/dt+ 1/LC du/dt + u= E/LC

Mais là je ne suis pas du tout sure de ma réponse :/ dois remplacer encore 1/LC par 1 ??

Q6: Montrer que la tension u s'écrit pour t<0 : u(t)= U₁ exp(t)cos(t+)+ U2
en déterminant alpha, beta et U2

R7: ici je ne vois pas comment me ramener à l'expression de cos(t+), je dois me mettre dans un régime sinusoïdal forcé?

Q7:Montrer grâce aux conditions initiales en t=0+ que = /3 en déduiree l'expression de U1

Q8: Tracer l'allure de la courbe u(t) pour t>0
R8: je n'ai pas fait les questions d'avant donc un peu dur de faire celle ci ^^

Voilà si vous pouviez m'éclairer

Pas de réponses? ou le sujet ne remonte pas étant trop ancien?