Inscription / Connexion Nouveau Sujet
oscillateurs électriques : circuit RLC
Bonjour,
J'ai besoin de votre aide pour cet exercice sur les oscillateurs électriques.
EXERCICE
Un circuit électrique comporte : une bobine de résistance R , une source de tension u(t)=50√2sin(wt)
(la pulsation w est réglable),
un ampèremètre donnant l'intensité efficace I, d'impédance négligeable.
Lorsque w=10³ rad/s , I=0,1A .
1) - Calculer l'inductance de
la bobine, le déphasage de la
tension par rapport à
l'intensité.
- Écrire l'expression de
l'intensité instantanée .
2)- Quelle capacité C faut-il
placer en série avec la bobine
pour que l'intensité soit en
phase avec la tension aux
bornes de l'ensemble ?
- Quelle est alors l'intensité
efficace Io ?
- Déterminer les tensions
efficaces Ub et Uc aux
bornes de la bobine et de la
capacité.
- Évaluer le rapport Q=Uc/U.
[Mon début]
1) ★Calcul de l'inductance de la bobine:
Sachant que la réactance de la bobine est R'=L*w ; la tension efficace U y vaut U=L*w*I .
L=U/(w*I) . Or Umax= 50√2 V => U=50 V . Donc L=50/(10³*0,1)= 0,5 H.
★ Déphasage:
En faisant une construction de Fresnel, le déphasage ∅ est tel que :
sin∅=Z/(L*w) où Z est l'impédance du circuit: Z=U/I =500 ohms
=> sin∅=500/(0,5*10³)=1 soit ∅=π/2 rad.
★ Intensité instantané :
Son expression est de la forme I(t)=Imax*sin(wt+∅') .
I=0,1 A => Imax=0,1√2 A. En supposant que la tension est en avance de phase sur elle, et que sa phase est nulle, ∅'=-π/2 (?)
=> I(t)=0,1√2*sin(1000t-π/2)
2) ★Capacité à placer:
L'intensité et la tension étant en phase, le circuit est en résonance d'intensité :
1/c*w = L*w <=> C=1/(L*w²)= 2 uF.
★Ici je ne sais vraiment pas quelle piste emprunter ,,, je pensais à égaliser les phases de I(t) et U(t) pour avoir la valeur de t et la remplacer dans i(t) pour avoir Io...
je pensais à égaliser les phases de I(t) et U(t) pour avoir la valeur de t et la remplacer dans i(t) pour avoir Io...
Bonjour
Première question : l'énoncé parle de bobine de résistance R. Cette résistance est-elle négligeable devant la réactance ? Le rapport des valeurs efficaces U/I est l'impédance dans le cas général, pas la réactance.
La suite laisse penser logiquement que la résistance de la bobine n'est pas négligeable. Et pourtant : rien dans l'énoncé ne permet d'obtenir sa valeur... Relis attentivement l'énoncé original pour vérifier que tu n'as rien oublié lors de ta copie sur le site.
Sinon, s'il s'agit d'un simple exercice d'entraînement, je te suggère de choisir : R=400 . Tu vas constater que cela conduit à des valeurs numériques simples pour la suite...
. Tu vas constater que cela conduit à des valeurs numériques simples pour la suite...
Oui c'est juste un exercice d'entraînement .
La tension aux bornes de la bobine est U=R*I + L*dI/dt
<=> U/I = R + (L/I)*di/dt
Z=R+(L/I)*di/dt
=> L=(I(Z-R))/(di/dt)
Que vaut Z et di/dt ...
Pour representer les vecteurs associés aux tensions aux bornes du circuit?
Dans le cours, nous avons aussi vu cette relation Z²=R²+(Lw)²
Tu étais bien parti dans ton message de 14h46. Si on pose :
Cela conduit au diagramme de Fresnel ci-dessous (mon logiciel a mal dessiné la lettre grecque  mais cela ne devrait pas gêner la compréhension).
mais cela ne devrait pas gêner la compréhension).
Ce diagramme permet de retrouver l'expression de l'impédance Z que tu viens de rappeler et il permet aussi d'obtenir la valeur de  .
.
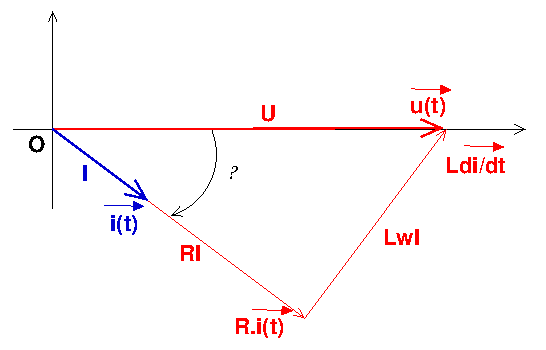
En appliquant la propriete de Pythagore dans le triangle rectangle, on a:
U²=(RI)²+(LwI)²
U²/I²= R²+(Lw)² soit
Z=√(R²+(Lw)²).
sachant que I=0,1 V et U=50 V ; Z=50/0,1=500 Ω,
De la relation precedevnte, L=√((Z²-R²)/w²)
soit L=0,3 H
ok.
'2)L'intensité et la tension sont en phase lorsque tanφ=0 ( , la capacité étant en série avec la bobine la construction de Fresnel dans le cas géneral donne tanφ=(Lw-1/(Cw))/R ) soit Lw=1/Cw <=> C=1/(Lw²)=1/(0,3*10^6)≈ 3,33 μF
* Intensité du courant :
U(t) et I(t) sont en phase : la résistance du circuit est égale à son impédence et le circuit se comporte comme un conducteur ohmique. Z=R=U/Io
Puis je écrire Io=U/Z ?
Oui mais avec Z=R. Tu vas obtenir une valeur de Io supérieure à la valeur de I obtenue en absence de condensateur. N'oublie pas que j'ajout du condensateur à conduit à une situation de résonance d'intensité.
I=U/Z . En dérivant I par rapport au temps, on trouve 0.
di/dt=0 <=> I√2cos(ωt-φ)=0
=> ωt-φ=π/2 + 2κπ , k ε Z.
, ωt=π/2 +φ +2kπ => t=(π/2+φ+2kπ)/ω.
Ainsi pour ce temps t, correspond un courant i(t)=I√2sin(ω(π/2+φ+2kπ)/ω -φ)=I√2 soit Io=0,1*√2≈0,14 Α
On ne te demande pas à quelles date i(t) passe par un maximum. Il suffit de raisonner sur les valeurs efficaces et l'impédance.
A la résonance d'intensité : Z=R donc, en valeurs efficaces :
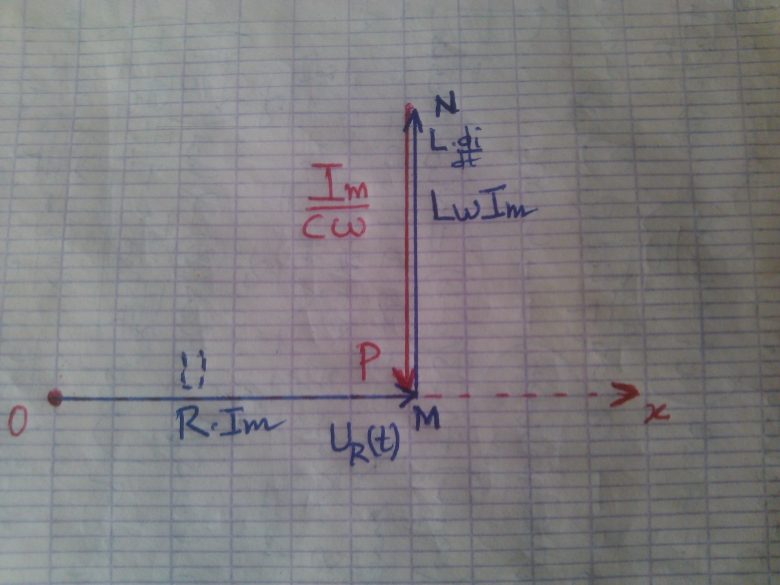
Restent les tensions efficaces aux bornes de L et de C. On peut raisonner avec les impédances. Un tracé des vecteurs de Fresnel dans ce cas particulier de la résonance d'intensité aide à bien comprendre.
On a les tensions:
qui est représentée par le vecteur OM;
représentée par le vecteur MN ;
, représentée par le vecteur NP.
Leurs phases étant toutes diminuées de φ, je ne l'ai pris en considération lors de la construction.
tension U(L) aux bornes de la bobine :
U(L)=R.I + Ldi/dt <=> À la phase de résonance, di/dt=0 <=> U(L)=RI=400*0,125=50 V ...ce qui semble être ambigu vu que ces dipoles sont en série et que le générateur fourni 50 V
Dans le cas particulier de la résonance d'intensité, tension instantanée u(t) et intensité instantanée i(t) sont en phase (  =0)
=0)
En régime sinusoïdal, chaque tension instantanée et l'intensité instantanée varie en fonction du temps de façon sinusoïdale et présente donc un maximum et un minimum par période. La dérivée de l'intensité instantanée s'annule donc deux fois par période. Cela n'a rien à voir avec le phénomène de résonance d'intensité où on s'intéresse au maximum de l'intensité efficace lors que l'on fait varier la pulsation. On s'intéresse donc à l'expression générale de l'intensité efficace :
On considère U constant et on s'intéresse aux variations de l'intensité efficace I en fonction de  et on montre qu'il existe un maximum d'intensité efficace lorsque
et on montre qu'il existe un maximum d'intensité efficace lorsque  =
= o avec
o avec .Ce maximum correspond à une dérivée nulle de l'intensité efficace par rapport à
 :
:
à la résonance d'intensité. Cela n'a rien à voir avec le
donc il a été question dans la première partie de mon message ! Il est fondamental de bien faire la différence entre les valeurs efficaces et les valeurs instantanées.
Donc on a I est maximale lorsque Z est minimale. Et Z est minimale lorsque Lw=1/Cw <=> Lcw²=1
En dérivant donc l'expression de I par rapport à ω je trouve:
Cette dérivée s'annule en w=1/√(LC) et w=-1/√(LC).
Désolé, mais jusque là je n'arrive pas ressortir un lien avec la tension aux bornes de la bobine ...
Le but de mon précédent message était de bien t'expliquer la différence entre la condition de résonance d'intensité : où on raisonne sur la valeur efficace de l'intensité et l'existence de maximums et de minimums de l'intensité sinusoïdale instantanée qui correspondent à
Je n'y suis pas arrivé car tu écris à 22h16 :
alors qu'il aurait fallu écrire :
Je me répète :
Il est fondamental de bien faire la différence entre les valeurs efficaces et les valeurs instantanées.
Sinon, pour les tensions efficaces Ub et Uc, il suffit d'interpréter le diagramme de Fresnel de ton message du 28-03-21 à 16:47.
Il est fondamental de bien faire la
différence entre les valeurs efficaces et
les valeurs instantanées.
C'est ce qui m'échappe souvent surtout quand il s'agit des applications.
Ok je vois...
Sur le diagramme, les vecteurs representant les tensions Ub et Uc ont la même norme mais de sens contraire.
Im/cw = LwIm
UL(t)=LwIm*sin(wt+π/2)
Uc(t)=LwIm*sin(wt-π/2)
Il me semble que ces deux tensions sont égales en norme ...mais seulement que l'une est l'opposé de l'autre à chaque instant.
Habituellement les grandeurs instantanées sont symbolisées par des minuscules. Pour plus de clarté, on ajoute souvent la mention "(t)". Les grandeurs indépendantes du temps : les amplitudes et les valeurs efficaces sont symbolisées par des majuscules.
Ici : Ub et Uc désignent respectivement les valeurs efficaces de uL(t) et de uc(t).
Compte tenu de ces valeurs instantanées :
Les valeurs efficaces sont :
D'accord.
Ub=LwIo=0,3*1000*0,125=37,5 V.
De même Uc=37,5 V.
★Evaluation du Rapport Q.
!
Q=Uc/U=37,5/50≈0,75 soit Uc représente 75% de la tension aux bornes du générateur. On peut dire qu'il n'y a pas une surtension.
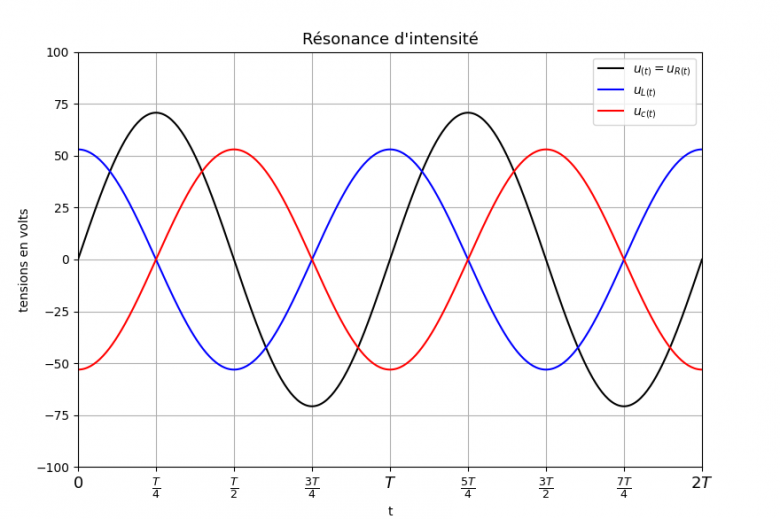
Pour t'aider à mieux comprendre, voici représentées graphiquement les variations en fonction du temps des trois tensions instantanées :
1° : u(t)=uR(t) (égalité valide seulement à la résonance d'intensité) en noir
2° : uL(t) en bleu ; noter que cette tension est en avance d'un cquart de période par rapport à u(t)=uR(t) : les valeur nulles d'une tension instantanée correspondent à des maximums ou des minimum de l'autre tension instantanée
3° : uc(t) en rouge ; noter que cette tension est en retard d'un quart de période par rapport à u(t)=uR(t). Cette tension se trouve en opposition de phase par rapport à uL(t) : les valeurs nulles des deux tensions instantanées sont obtenues aux mêmes instants et à un maximum d'une tension correspond un minimum de l'autre.
Une remarque à propos de Q. Ce coefficient est appelé coefficient de surtension mais la surtension existe seulement pour une résonance d'intensité assez aiguë donc une résistance plutôt faible. Ce n'est pas le cas ici.
À partir du diagramme de Fresnel, on montre facilement :
Q=L. o/R
o/R
ok je vois...Au cours on l'avait ( Q) nommé ''facteur de qualité'' et est egal au rapport de la pulsation à la résonance par la largeur de la bande passante Δω.
Q=ωο/Δω qui conduit à la relation que vous avez écrite en utilisant la relation Δω= R/L dont je ne sais d'ailleurs d'où ça vient...
dont je ne sais d'ailleurs d'où ça vient...

 =
= 2-
2- 1 où
1 où  2 et
2 et  1 sont les deux pulsations pour lesquelles
1 sont les deux pulsations pour lesquelles Je te laisse démontrer, si cela t'intéresse que ce sont les deux racines positives de l'équation :
Plus le facteur Q est élevée, plus

 est faible, plus la résonance est aigüe. Comme déjà dit, une valeur élevée de Q suppose une résistance R nettement inférieure à L
est faible, plus la résonance est aigüe. Comme déjà dit, une valeur élevée de Q suppose une résistance R nettement inférieure à L o, ce qui n'est pas le cas avec ces valeurs numériques.
o, ce qui n'est pas le cas avec ces valeurs numériques.cela est peut être dû aux données de l'énoncé ...
L'expression de l'impédance étant Z=U/I et qu'à la résonance Io=U/R : on a : I=U/Z .
w2 et w1 étant les pulsations pour lesquelles I=Io/√2; on a donc U/Z=U/R√2 <=> Z=R√2
<=>
<=> soit
Cette équation est équivalente aux équations:
(1) Lw- 1/cw= R
(2) Lw- 1/cw=-R
(1) conduit à l'équation du second degré Lcw²-Rcw-1=0 dont le discriminant est D=R²c²+4cL. Elle admet comme solution positive w1=(RC+√D)/2Lc .
La solution positive de (2) est :
w2=(-Rc+√D)/2Lc.
La difference entre la plus grande valeur de la pulsation (w1) et la pulsation w2 donne ♦w=2Rc/2Lc .
Soit ♦w=R/L.
D'accord avec ton calcul.
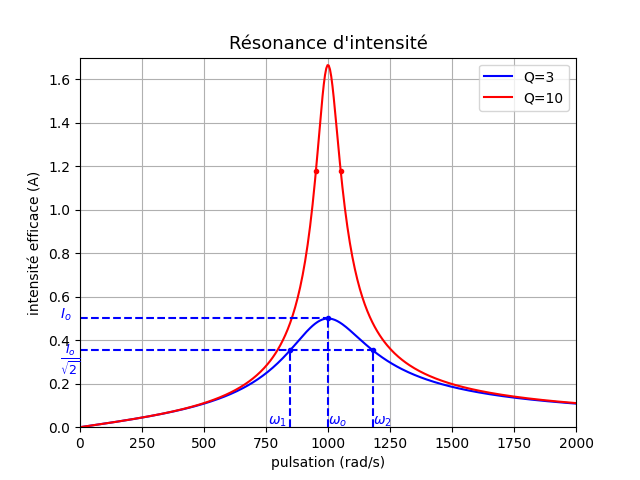
Pour illustrer l'influence du facteur Q sur l'acuité de la résonance d'intensité, voici deux courbes représentant les variations de l'intensité efficace en fonction de la pulsation pour les valeurs de L et C de ton problème, pour deux valeurs différentes de la résistance correspondant à deux valeurs de Q différentes : 3 et 10.
J'ai placé les pulsations limites  1 et
1 et  2 pour Q=3 (courbe bleue)
2 pour Q=3 (courbe bleue)
Pour ne pas surcharger la figure, je me suis contenté de placer deux points rouges sur la courbe correspondant à Q=10 aux deux pulsations limites. On voit bien que 
 =
= 2-
2- 1 est nettement plus faible pour Q=10.
1 est nettement plus faible pour Q=10.
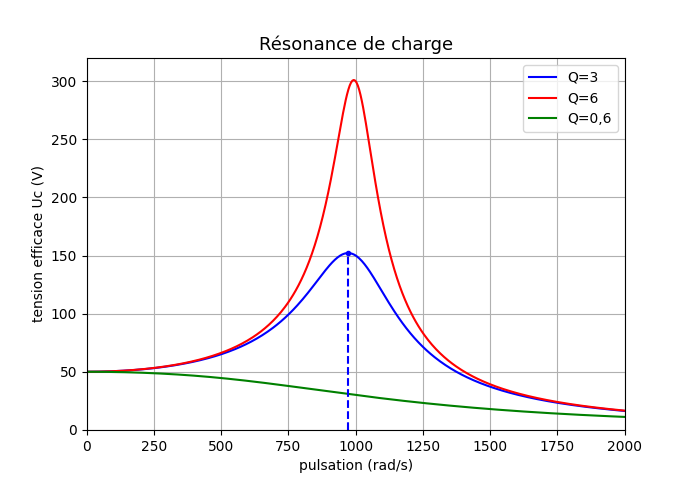
Une dernière remarque puisque ton énoncé parlait de surtension aux bornes du condensateur. J'ai représenté ci-dessous la courbe représentant les variations de la tension efficace Uc aux bornes du condensateur en fonction de la pulsation  . J'ai conservé les valeurs de L et C, donc toujours :
. J'ai conservé les valeurs de L et C, donc toujours :  o = 1000rad/s avec comme valeur efficace de la tension d'alimentation : U=50V. J'ai choisi trois valeurs différentes de R correspondant aux trois valeurs de Q indiquéesen légende des courbes. On vérifie facilement dans les trois cas : Uc=Q.U si
o = 1000rad/s avec comme valeur efficace de la tension d'alimentation : U=50V. J'ai choisi trois valeurs différentes de R correspondant aux trois valeurs de Q indiquéesen légende des courbes. On vérifie facilement dans les trois cas : Uc=Q.U si  =
= o mais cela ne correspond pas nécessairement à une surtension, ce qu'on appelle encore une résonance de charge, (expression en rapport avec la charge du condensateur). En réalité, on démontre au niveau (bac+1) que l'existence d'un maximum de Uc n'est possible que pour
o mais cela ne correspond pas nécessairement à une surtension, ce qu'on appelle encore une résonance de charge, (expression en rapport avec la charge du condensateur). En réalité, on démontre au niveau (bac+1) que l'existence d'un maximum de Uc n'est possible que pour . Sinon, Uc est fonction monotone décroissante de
 (voir courbe verte).
(voir courbe verte).
On peut aussi noter d'autres différences significatives entre ce phénomène et celui de résonance d'intensité :
- Quand 
 0, Uc
0, Uc U alors que l'intensité efficace tend vers zéro quand la pulsation tend vers zéro.
U alors que l'intensité efficace tend vers zéro quand la pulsation tend vers zéro.
- Quand la résonance de charge existe, elle à lieu pour une pulsation un peu inférieure à  o et non égale à
o et non égale à  o comme pour la résonance d'intensité.
o comme pour la résonance d'intensité.
PS : si gbm a l'occasion de lire ce message (bonjour à lui !), il comprendra la corrélation entre cette résonance de charge et le phénomène de résonance d'amplitude en mécanique dont nous avons parlé récemment à propos d'une certaine fiche ...