Inscription / Connexion Nouveau Sujet
Oscillateur mécanique.
Bonjour,
Merci d'avance. 
Au cours d'une séance de travaux pratiques, votre professeur réalise avec vous l'expérience de la figure ci-dessous pour montrer la conservation de l'énergie mécanique.
Le pendule élastique est constitué par un solide (S) de masse m 0,2 kg , soudé à l'une des extrémités d'un ressort (R) à spires non jointives de masse négligeable et de constante de raideur k, l'autre extrémité étant attachée à un support fixe.
A partir du point O , le solide (S) est écarté vers un point A d'abscisse , et a la date t = 0 s , (S) est abandonné à lui-même sans vitesse initiale.
Au cours de son mouvement le solide (S) se déplace sans frottement et son centre dinerie G est repéré par l'élongation OG= x(t).
À l'équilibre le centre d'inertie de (S) coincide avec le point O , origine de l'axe orienté (x' ; x). L'enregistrement des
variations de l'élongation x au cours du temps est représenté par l'oscillogramme
ci-dessous.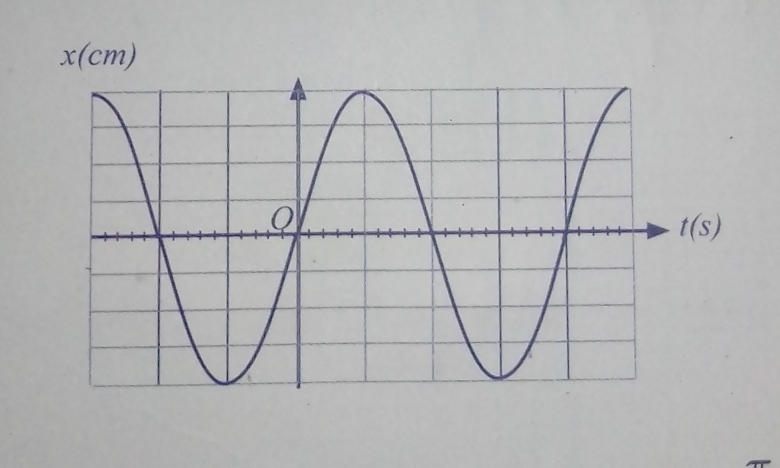
et
1) Donne les caractéristiques générales d'un oscillateur mécanique.
2) Déduis de l'oscillogramme :
2.1) l'amplitude des oscillations ;
2.2) la période propre des oscillations.
3. Écris la loi horaire du mouvement du solide.
4. Montre que l'énergie mécanique est constante.
Réponses
1) Les caractéristiques générales d'un oxillateur mécanique sont :
L'amplitude maximale ;
La pulsation propre du ressort ;
La phase a l'origine ;
La periode propre.
2-1) On compte quatre divisions.
Xm=4 cm.
Donc Xm= 4.10-2m.
2-2) On compte 10 divisions.
3) L'équation horaire du mouvement de ce solide est donnée par :
Car sa courbe est celle d'une fonction sinusoïdale impaire. (Sinus)
Xm= 4.10-2 m car
D'où
2-2) On compte 10 divisions.
Où voyez-vous 10 divisions ?
Car sa courbe est celle d'une fonction sinusoïdale impaire. (Sinus)
Oui, donc
: vous dites vous-même que c'est un sinus.Oui, donc
: vous dites vous-même que c'est un sinusC'est faux ?
Comment est-ce que je devrais faire ?
Vous dites que c'est un sinus, ce qui exact ; pourquoi ajouter vous un ?
Autre solution, vous dites que c'est de façon générale une fonction sinusoïdale et de la même manière que vous avez déterminé
et Xm, vous déterminez en prenant un point particulier, le plus simple étant en t=0.
Mais la solution la plus simple, c'est celle que vous avez prise : c'est une fonction sinusoïdale impaire, donc un sinus et par définition, la fonction sinus est la fonction x -> sin(x).
Moi j'ai compris les petits traits verticaux.
La division concerne les grands traits (les petits sont appelés subdivisions)
Mais une période n'occupe pas 10 petits intervalles, mais combien ? Autrement dit quelle est la définition d'une période ?
Vous dites que c'est un sinus, ce qui exact ; pourquoi ajouter vous un
?Je ne comprenais pas pourquoi je ne devrais pas ajouter
2-2) On compte 2 divisions.
3) L'équation horaire du mouvement de ce solide est donnée par :
Car sa courbe est celle d'une fonction sinusoïdale impaire. (Sinus)
Xm= 4.10-2 m
D'où
Ce n'est pas vraiment la définition d'une période, la définition d'une période fait intervenir un point quelconque, en prenant votre vocabulaire :
"La période est le temps mis par l'oscillateur pour revenir à un point quelque soit ce point".
Pas vraiment, l'oscillateur passe bien en 0 à t=0 et deux divisions plus tard, mais j'ai déjà indiqué que ce n'était pas la définition de la période, cela doit marcher pour tous les points.
Si vous prenez le passage au maximum (à t=1div), le point ne repasse pas au maximum à t=1+2=3 div, doc 2 div n'est pas la période.
Donc ici la période est ?
s.Oui donc
3) L'équation horaire du mouvement de ce solide est donnée par :
puisque La courbe représentative du système indique que la phase à l'origine
(au point O).
Annuler
connectez vous