Bonsoir,
J'ai besoin de votre aide en passant en «revue» ce que j'ai fait sur cette exercice :

Deux microphones M1 et M2, distants de d, sont placés dans l'axe d'un haut parleur émettant un son sinusoïdal de fréquence N comme l'indique la figure ci-dessous.
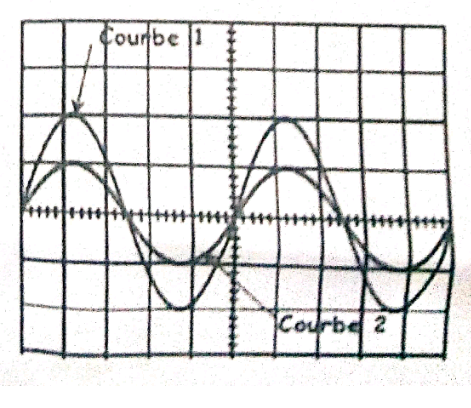
Les microphones M1 et M2 étant connectés respectivement aux voies B et A réglées sur la même sensibilté verticale. Le balayage horizontal est: 0,25 ms/division.  On obtient amors l'oscillogramme representé ci-dessous.
1. Identifier en justifiant la voie correspondant à chaque courbe de l'oscillogramme.
2.Déterminer la fréquence de l'onde sonore.
3.La distance minimale entre les microphones pour laquelle les deux courbes sont en phase est d_min=42,5 cm.
3.1) déterminer la longueur d'onde de l'onde sonore.
3.2) En déduire la célérité du son dans l'air.




1. Pour cette question, l'oscillogramme présente deux courbes d'amplitudes différentes: L'amplitude de la courbe 1 est supérieure à celle de la courbe 2.
Sur la figure, le microphone M1 associé à la voie B est plus proche du haut-parleur. L'amplitude serait alors influencé par la distance Haut-parleur<>Microphone...j'ai alors opté pour les choix:
Voie B: courbe1
Voie A: courbe2.

2. Graphiquement une période correspond à 5 divisions.
T=0,25*10^(-3)*5=0,00125 s.
Soit N=1/T=800 Hz.

3.1) En posant d1=M₁H où H est la position du haut parleur et d2=M₂H ; la difference de marche est d=d2-d1.
Sachant que M1 et M2 sont en phase, d2-d1=k*L où k est un entier et L , la longueur d'onde de la vibration sonore. d étant minimal, k prend la valeur 1 .
Pour k=1, L=d2-d1=d_min=0,425 m.

3.2) célérité du son dans l'air :
Par définition, elle est homogène à la longueur d'onde sur la fréquence du son,  donc C=L/T soit
c=L.N=0,425*800=340 m/s