s'il vous plait

Bonjour zaki31,

je ne vois pas ou est la difficulte : sur la photo, entre le bord gauche ou se trouve la source S et le bord droit, je compte 13 longueurs d'ondes, etalees sur la largeur de 12,5 cm : donc = 12,5 : 13 = 0.962 cm.

Ensuite, en effet = c/F donne c = .F = 0.962 x 0.4 = 0.385 cm/s.

Entre deux points A et B distants de 15 cm, il y a 15/0.962 = 15.6 longueurs d'onde. Les points qui ont le meme etat vibratoire sont ceux qui sont separes d'un nombre entier de longueurs d'onde. On oublie donc le 15 pour ne s'interesser qu'a la partie decimale du resultat precedent, cad 0.6. Sachant que un ecart en distance de 1 longueur d'onde correspond a un dephasaged e 360 degres ou 2 radians, un ecart de 0.6 longeuur d'onde correspond a un dephasage de 216 degres ou 1.2 radians (tu fais le produit en croix). Si B est atteint pas l'onde apres le point A, la vibration  du point B est en retard sur celle de A, ce retard se traduit par un retrd de phase de - 216 degres. Ca veut dire que si on ecrit la vibration de A comme s_A = S₀.cosx, ou x est une variable dependant de t et exprimee en degres, alors la vibration de B s'ecrit s_B = s₀.cos(x - 216). Dans ces expressions s0 est l'amplitude de la vibration imposee par le deplacement du stylet qui plonge dans l'eau (non donnee ici, donc tu peux faire s₀ = 1 cm sans risque, ca n'a pas d'importance).
Il ne te reste plus qu'a representer les deux fonctions s_A(x) et s_B(x) sur le meme graphique, en faisant varier x entre 0 et 360 degres.

Je ne vois qu'un pb a cetb exercice : les valeurs ne sont pas realistes. En effet, 0.4 Hz veut dire que la periode de la vibration est T = 2.5 seconde. Or, il suffit de frapper la surface de l'eau toutes les 2,5 secondes pour constater que la distance entre les maximums est bien superieure a 0.9 cm, et donc que l'onde se deplace a une celerite bien plus grande que celle que j'ai calculee. Fais l'experience dans une baignoire... Je me suis peut-etre trompe dans le calcul mais je ne vois pas ou. Pour moi, c'est la frequence qui est fausse : peut-etre 40 Hz au lieu de 0.40 Hz ? verifie ton enonce stp.

Si tu as des questions n'hesite pas a continuer a poster.

Prbebo.

Merci beaucoup,

Par contre je suis vraiment désolé j'ai fait une erreur la distance séparant A et B n'est vaut pas 15 cm mais 3.15 cm  

En rectifiant je trouve qu'il y a donc 3.274 longueurs d'ondes.
Les points qui ont le même état vibratoire sont ceux qui sont separes d'un nombre entier de longueurs d'onde. On oublie donc le 15 pour ne s'interesser qu'a la partie decimale du resultat precedent, cad 0.274. Sachant que un ecart en distance de 1 longueur d'onde correspond a 360 degres ou 2 radians, un ecart de 0.274 longeuur d'onde correspond a 98.64 degres ou 1.722 radians.

Par contre pour le reste je ne comprend absolument rien  
Qu'est ce qu'un dephasage ?

Bah, ca ne change rien a mon raisonnement mais simplement les valeurs numeriques sont modifiees : AB/3.15  / 0.962 = 3.27 longueurs d'onde. On oublie le 3 et on transforme la partie decimale 0.27 en degres en faisant un produit en croix (1 = 360 degres, donc 0.27 = ?).

Je persiste a dire que les valeurs de l'enonce (0.40 Hz pour la frequence ou 12.5 cm pour 13 longueurs d'onde) ne sont pas eralistes.

Prbebo.

Je sais pourquoi tu ne comprends pas, et tu n'es pas le seul dans ce cas : c'est parce que le programme de physique de TS est tellement absurde qu'on oblige les eleves a travailler avec des fonctions du temps (propagation d'une onde sinusoidale, addition pour obtenir des interferences etc...) sans jamais ecrire explicitement ces fonctions. En tout cas, dans le bouquin que j'ai (Nathan, physique-Chimie TS nouveaux programmes), je ne les ai vues nulle part.

Alors pas de panique, car ce n'est pas vraiment complique :
imagine un point S de l'espace qui emet une vibration sinusoidale, de periode T et donc de frequence f = 1/T. La vibration de S peut s'ecrire en fonction du temps t a l'aide d'une fonction sinus ou cosinus (tu verras plus tard qu'on prefere le cosinus). Donc on ecrit s(t) = s₀.cos(t), ou S₀ est l'amplitude de la vibration.
1ere question avant de continuer : sais-tu comment on appelle la grandeur qui figure dans la parenthese, et en quelle unite se mesure-t-elle ?

Non désolé je ne vois pas .

Oui, je m'attendais un peu a cette reponse... t est un angle (puisqu'on en prend le cosinus) donc qui se mesure en degres, ou (mieux) en radians. Donc la quantite se mesure en radians par seconde. On l'appelle "vitesse angulaire", puisqu'elle exprime la vitesse avec laquelle l'angle = t varie, ou encore "pulsation".
Cette constante est reliee a la periode T de la vibration de la source S : en effet, au bout d'une periode T la vibration s(t) reprend la meme valeur (par definition de T). L'angle qui figure dans le cosinus a augmente de 2 radians (puisque le cosinus reprend la meme valeur) ; donc on peut ecrire (t + T) = t + 2, ce qui donne T = 2 soit = 2/T ou encore = 2.f .  Avant de continuer, est-ce OK ?

Ouais je pense avoir compris

zaki31, j'attends ta reponse avant de continuer. Mais, comme on arrive dans des heures ou il faut aussi diner, si tu veux on peut reprendre la discussion dans 1 heure, vers 20h30.
Ce qui va t'arriver ensuite : maintenant que j'ai defini la constante , je vais t'expliquer ce qu'est un dephasage, en comparant les vibrations l'une issue de la source S et l'autre qui atteint un point M quelconque.
Je t'ecoute.

Ah bien ! Alors rassure-toi, la suite n'est pas difficile non plus :

Le prends un point M de l'espace situe a la distance SM = d de la source S. Comme dit precedemment, la source S emet une vibration qui s'ecrit s(t) = S₀.cos(t), avec = 2/T ou T est la periode de cette vibration.
Si cette vibration se propage avec la celerite c, il va lui falloir un certain temps pour atteindre le point M et le mettre en vibration lui aussi : es-tu d'accord pour dire que ce temps, que j'appelle , depend a la fois de la celerite c et de la distance d a parcourir, et qu'il s'ecrit d/c ?

Je t'ecoute.

Oui pour l'instant je suis d'accord et je comprend.

Ouf ! j'ai eu peur que tu ne te sois sauve... dans mon message ci-dessus, tout a la fin, il faut lire = d/c. Le signe = est passe a la trappe, mais je pense que tu as compris.
Alors, voici maintenant la derniere question :
Je cherche a ecrire la vibration qui arrive en M en fonction du temps, et que je vais noter s_M(t). Et je dis que la vibration qui arrive en M a l'instant t est celle qui a quitte la sourve S a l'instnt t - , ou est le temps qu'il lui a fallu pour parcourir la distance d = SM (si cette phrase n'est pas claire, pense au rayonnement qui nous vient d'une etoile lointaine : nous recevons son rayonnement a l'instant t sur Terre, mais nous la voyons comme elle etait au temps t = , puisqu'il a fallu un temps pour que son rayonnement nous parvienne).
OK ?

OK c'est bon pour l'instant.

ben c'est bien, car dans le post ci-dessus il y avait aussi une faute de frappe : derniere ligne, il faut lire t - au lieu de t = q

Ouais j'ai vu mais j'ai pris compris qu'avec l'exemple concret du 1

desole zaki31, mais ma machine a plante severe, et j'ai du repartir du debut... je continue donc, en espereant etre tranquille de ce cote-la :
La vibration en M s'ecrit donc s_M(t) = S₀.cos[(t - )] (dans s(t) je remplace t par t - ), ce qui donne s_M(t) = S₀.cos(t - ) = s₀.cos(t - ), avec = .
Eh bien tu vois, l'angle s'appelle "dephasage" entre la vibration qui est partie de la source S et celle qui est arrive en M. Cet angle se mesure bien sur en radians. Le signe moins indique que la vibration arrivant en M est en retard sur celle qui est partie de la source S.
On peut donner l'expression de en fonction de la distance d et de la longueur d'onde : = avec = 2/T et = d/c, ce qui fournit = 2.d/(cT), mais par definition on appelle longueur d'onde la distance parcourue pendant une periode T avec la celerite c, donc = cT. Ce qui donne = 2d/, es-tu d'accord ?

C'est cette relation qu permet de tout comprendre sur la propagation des ondes sinusoidales ! En effet, imagine que l'on se place a l'instant t en un point M fixe (donc, d est fixe) : la vibration qui arrive en M reprendra la meme valeur aux instants t', t" etc..., tels que = 2, 4 etc... on a deja vu plus haut que ca implique = 2, 4 etc.., ce qui avec = 2/T donne t' = t + T, = t + 2T etc... En un point donne M, l'onde presente ainsi une periode temporelle T.

Maintenant, supposons qu'on prenne une photographie de cette onde, ainsi qu'on a fait sur la photo de ton post : cette fois, on a fixe un instant t particulier (celui ou on a pris la photo) et on regarde la structure spatiale de cette onde : on voit qu'il y a des points qui ont le meme etat vobratoier que celui de S ; ils sont comme ci-dessus definis par des dephasages = 2, 4 etc..., mais cette fois c'est leur distance d a la source S qui varie. Or, 2..d/ = 2 pour d = , = 4 pour d = 2, etc... la photo montre alors une periodicite spatiale, correspondant a la distance .

As-tu tout compris ? Tout ceci decoule des questions-reponses qu'on s'est echangees precedemment.

Reprenons la relation = 2d/. je viens de dire que si = 2, soit d = , M et S ont le meme etat vibratoire. Allons plus loin : si d = /2, ca donne = et cos(t - ) = cos(t - ) = - cos(t) : la vibration en M vibre a l'oppose de celle qui a quitte la source S (l'une est maximum lorsque l'autre est minimum, et vice-versa). On dit que ces deux vibrations sont en opposition de phase. On peut facilement voir ces points sur la photo de ton post : ce sont ceux qui sont dans un "creux", compare a ceux qui sont sur une "crete".

Alors si on resume : sur la photo deux points A et B auront le meme etat vibratoire si leur distance est egale a , 2, ... un nombre entier de longueurs d'onde ; ils ont un etat vibratoire oppose (max pour l'un, min pour l'autre) si la distance qui les separe est /2, 3/2 ... un nombre impair de fois la demi longueur d'onde.

T'es toujours la ?  Alors pour les points qui ne sont pas dans le deux cas ci-dessus, on connaitra leur etat vibratoire en comptant le nombre entier de longueurs d'onde dans la distance qui les separe : exemple, on a trouve entre A et B une distance de 3.27 longueurs d'onde, la question est : comment vibre B par rapport a A ?
Chaque longueur d'onde entiere correspond a une vibration de meme nature. Donc on enleve la partie entiere (3) de ce nombre et on ne retient que la partie decimale, soit 0.27. Puis on fait une "regle de trois", ou un "produit en croix" :
une longueur d'onde correspond a un retard de phase de 2 de B par rapport a A ; donc 0.27 longueur d'onde correspond a un retard de phase de 2x 0.27, soit 1.7 radians ou encore 97 degres. Le point B presente sur A un retard de phase de 97 degres, ce qui signifie que si on ecrit la vibration de A comme s₀.cos(x), celle de B s'ecrit s₀.cos(x - 97).
Maintenant, tu comprends que cette variable x est egale a t, mais comme tu vas faire un dessin sur une feuille de papier il est plus simple de confondre la variable temporelle t en une variable spatiale x.

Bon, je ne pensais pas etre aussi bavard ! Retiens bien les relations que je t'ai expliquees : la definition de la pulsation et son expression en fonction de la periode T, et aussi le dephasage et la relation = 2d/. On se retrouvera peut-etre si tu mets un post concernant les interferences : tu verras alors que avec ces deux relations tout devient facile.

Bonne soiree,

B.B.

Il n'y a pas de soucis.

La par contre j'ai un peu de mal mais surtout le problème c'est que je ne vois pas ce que je dois réellement faire pour mon exercice même si en soi j'ai assez bien compris tout ce qui a était fait précédemment
.

Je comprends que ce soit dur a avaler d'un coup, surtout a cette heure-ci ! Alors on recapitule :
Suppose que le point A soit choisi de telle maniere qu'il ait le meme etat vibratoire que celui de la source S, c'est a dire s_A(t) = s₀.cos(t), a quelques 2 pres (cad, si A est distant d'une longueur d'onde de S sa vibration s'ecrira s₀.cos(t - 2), s'il est a la distance 2 de S elle s'ecrira s₀.cos(t - 4), etc...) et tous ces cosinus sont egaux a cos(t), car les angles correspondants different d'un nombre entier de fois 2). C'est cette quantite t que j'appelle x.
La vibration de B distant de A de 3.15 cm et en retard sur celle de A, ce retard ayant ete exprime ci-dessus a l'aide du dephasage = 1.7 radians ou 97 degres. Ca veut dire que si on ecrit s_A = s₀.cosx, on ecrira s_B = s₀.cos(x - 97) en exprimant x en degres (plus simple a tracer que x en radians). Ce sont ces deux fonctions que tu dois tracer.
Ci-dessous ce que ca donne avec excel : j'ai pris s₀ = 1 cm, en bl;eu c'est la vibration de A et en rouge celle de B, qui est retardee de 97 degres. J'ai fait le trqce sur deux periodes (x varie de 0 a 720 degres).

Je vais rendre d'antenne, si tu as encore des questions on verra ca demain.

Prbebo.

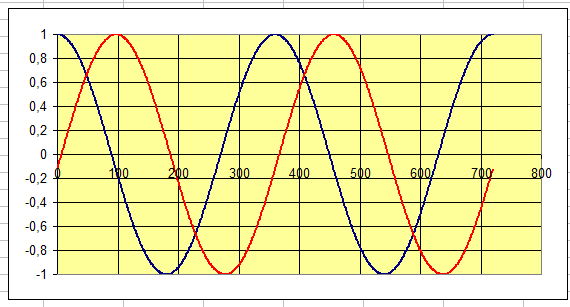
Je pense avoir assez bien compris.
Si je comprend bien, ce graphique est le graphique representant l'altitude de la surface de l'eau aux points A et B en fonction du temps?

En tout cas MERCI BEAUCOUP  pour votre aide.

C'est exactement ca. Maintenant que cet arrive a sa fin, permets-moi d'en faire le bilan :

En negatif :

1 - la celerite c = 0.385 cm/s, pour une frequence de 0.4 Hz, est anormalement faible. Pour moi, a tres basses frequences (0.40 Hz, c'est le cas), la vitesse de propagation des de l'ordre de 20 cm/s, soit 50 fois plus. Voir par exemple cette video . Il y a donc a mon avis un pb avec les valeurs numeriques donnees dans ton enonce.

2 - Je considere comme absurde, de la part d'un enseignant, d'obliger un eleve a tracer deux sinusoides retardees de 97 degres. 90 degres ou 180 degres (respectivement quadrature de phase et opposition de phase) a la rigueur je veux bien, mais 97... Mais peut-etre cela decoule-t-il d'une mauvaise valeur de la longueur d'onde due a l'erreur signalee ci-dessus.

En positif :

J'ai eu l'occasion de t'expliquer ce qu'est un dephasage, et de te donner l'expression de ce dephasage en fonction de la distance parcourue depuis la source : c'est = 2d/, avec un signe moins puisque le point ou on regarde la vibration est necessairement en retard sur celui qui a emis cette vibration.
Plus tard (mais c'est peut-etre maintenant), tu etudieras le phenomene d'interferences, ou on va regarder l'etat vibratoire d'un point atteint par deux vibrations qui n'ont pas parcouru le meme chemin : facile ! l'une aura parcouru le chemin d₁ depuis la source, et presentera le dephasage ₁ = 2.d₁/, l'autre aura parcouru le chemin d₂ et presentera le dephasage ₂ = 2.d₂/. Tu devrais comprendre facilement que l'etat vibratoire du point M qui recoit ces vibrations depend de la difference de phase = ₂ - ₁ = 2./, en posant = d₂ - d₁ que l'on appelle "difference de marche". Si les deux ondes presentent un difference de phase = 0, 2, 4 etc... 2k, les deux ondes s'additionnent leurs effets, cad que si ce sont des ondes lumineuses, on aura de la lumiere au point ou elles se rencontrent. Au contraire, si = , 3, ... (2k+1), ces deux ondes vibreront en opposition de phase donc soustraieront leurs effets, et on n'aura pas sde vibration (obscurite en cas d'ondes lumineuses).

Or, = 2/ = 2k equivaut a = k, et = (2k+1)/2 equivaut a = (2k+1)/2 : voici retrouvees les positions des points places sur des franges resspectivement brillantes puis sombres !

A bientot peut-etre si tu as encore des pb avec la physique.

Prbebo.

Sinon  cette onde est bien une onde périodique progressive?

bien sûr, puisqu'elle a une célérité c'est qu'elle progresse, par opposition aux ondes dites stationnaires qui oscillent sans se déplacer. Un petit coup de wikipédia pour compléter l'info : .

BB.