Inscription / Connexion Nouveau Sujet
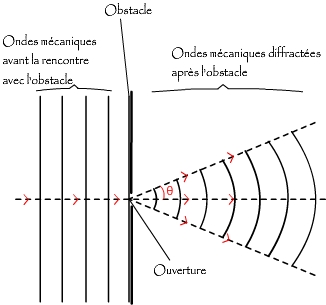
Onde mécanique progressive périodique
Bonjour à tous
J'ai un exercice merci beaucoup d'avance
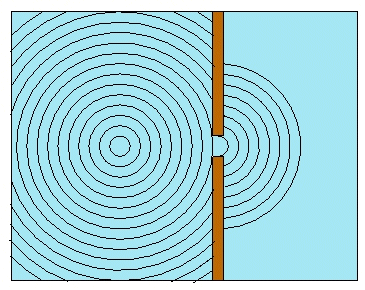
Dans le bassin d'eau on crée par un vibreur de fréquence réglable des ondes circulaires
progressives sinusoïdales. On éclaire le bassin par un stroboscope et on obtient un arrêt
apparent lorsqu'on règle la fréquence sur NS=10Hz .
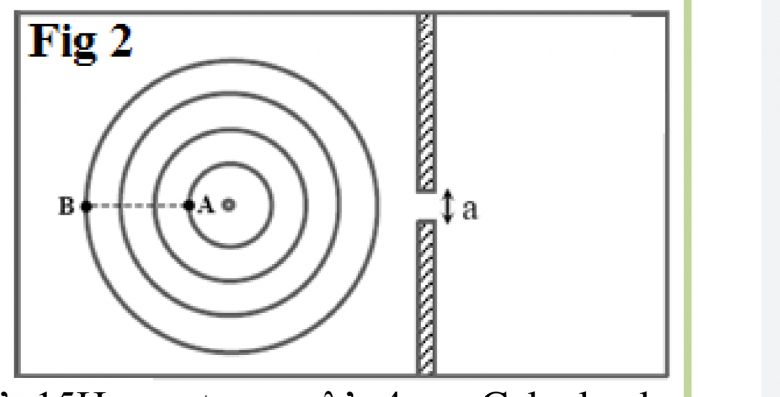
La figure 2 représente les lignes tel que AB=15cm.
On ajoute au bassin deux plaques distantes de a=2cm.
1-Déterminer la fréquence N ainsi la longueur d'onde λ et
déduire la célérité de propagation des ondes V.
2-Comparer l'état de vibration des points A et B.
3-Lorsqu'on règle la fréquence du vibreur sur la valeur N'=15Hz on trouve λ'=4cm. Calculer la
nouvelle célérité V' de propagation des ondes et la comparer avec V , conclure .
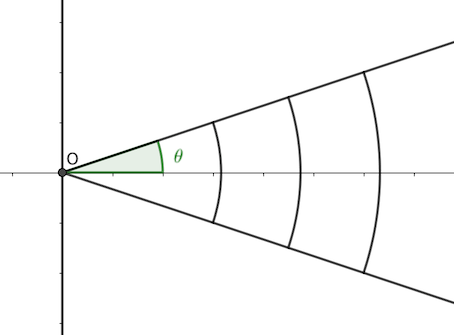
4-la fréquence est réglé à nouveau sur 10Hz ,recopier la figure 2 et représenter l'allure des ondes
après la traversée de la fente a et calculer l'écart angulaire θ.
Puis déduire l'angle de diffraction.
réponse
1) on a un arrêt apparait , c.à.d Ns=N . Donc N=10Hz
•
• V=
×N =0,05×10=0,5 m.s-1
2) on a AB/=0,15/0,05=3
Donc A et B sont vibrent en phases
3) V ' = ' / N '=
On remarque que V ' > V
Alors , on peut déduire que ce milieu est dispersif
4) 
L'écart angulaire :
=/ a=[0,05]\[2×10^{-2}]=2,2 rad
L'angle de diffraction : comment faire ?
Une petite indication s'il vous plaît merci beaucoup d'avance et comment représenter l'allure des ondes après la traversée de la fente
a
Merci beaucoup d'avance
Bonjour,
Question 2 : votre réponse est tautologique : vous avez utilisé AB pour calculer en s'appuyant sur le fait qu'ils sont dans le même état, et vous utilisez maintenant pour déterminer qu'ils sont dans le même état.
La réponse serait plutôt : le comportement de la lumière est le même dans les deux cas, donc même état de la surface de l'eau. Vous n'auriez pas interverti les questions 1 et 2 ?
Pour ce qui est de la représentation, vous avez un tout petit trou (), donc autrement dit un point qui émet des ondes et donc ... ?
Pour ce qui est des angles, vous êtes sûr du texte : quelle différence faites-vous entre l'écart angulaire et l'angle de diffraction ?
D'autre part votre relation est valable aux petits angles, 2,2 rad n'en est pas vraiment un.
Bonjour ,
Merci beaucoup de m'avoir répondu !
-J'ai utilisé les propriétés de la diffraction de l'onde .
Et s'est la réponse de :
(a < \lambda), donc autrement dit un point qui émet des ondes et donc diffracté
Vous n'auriez pas interverti les questions 1 et 2 ?
vous êtes sûr du texte : quelle différence faites-vous entre l'écart angulaire et l'angle de diffraction ?
J'ai copier coller le texte de l'énoncé , et c'est ça la question .
un point qui émet des ondes et donc diffracté
Pourquoi donc ? Le point au centre des cercles à gauche est bien un point qui émet des ondes et là pas de diffraction.
Il faut distinguer deux choses :
- la courbe que forme la crête des vagues : si toutes les vagues partent d'un même point, cette forme est ... ?
- l'étalement (dans quel endroit y-a-t-il essentiellement des vagues ?), et là c'est la diffraction qui commande.
Pour moi, mais je me trompe peut-être, pour répondre à la question 1, il faut savoir que A et B sont dans le même état (question 2).
Pour la fin, il faudrait retrouver dans votre cours les deux définitions de "écart angulaire" et "angle de diffraction".
Je n'ai pas dit qu'il n'y avait pas de phénomène de diffraction, mais que la forme des fronts d'onde (les traits noirs de l'image) n'avait pas de rapport avec la diffraction.
La diffraction est responsable de l'étalement, votre "écart angulaire" je suppose.
=143°Bonjour ,
(n'est vrai qu'aux petits angles)
Oui
Mon prof nous a dis d'utiliser cette relation
Merci beaucoup
Ici et donc la diffraction est "totale", i.e. l'onde envahit la totalité de l'espace à droite, donc ici l'angle de diffraction est
/2.
la relation donnant l'angle de diffraction est vraie aux petits angles.
Bonjour
Ici
/2. comment ?Merci beaucoup
i.e. = id est = c'est-à-dire.
Le 2 de /2 vient simplement du fait que l'angle de diffraction est défini comme le demi-angle d'ouverture ; ici l'ouverture est (le demi-espace à droite) et donc /2.
Bonjour :
/2 vient simplement du fait que l'angle de diffraction est défini comme le demi-angle d'ouverture ; ici l'ouverture est (le demi-espace à droite) et donc /2.=> Quel formule donne ce résultat ?
Merci beaucoup
Il n'y a pas de formule !
Simplement que la "formule" classique (exacte) ne fonctionne que jusqu'à =a (dans ce cas = /2), et qu'on ne peut pas avoir un angle plus grand à cause simplement de l'écran.
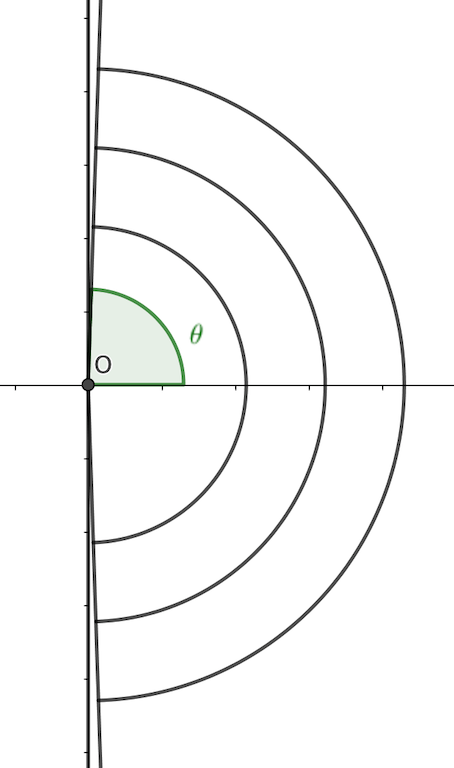
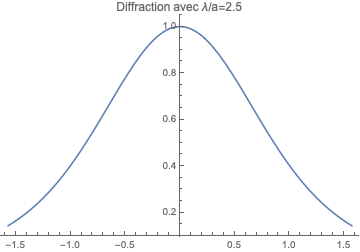
Dans la deuxième image, on rappelle la définition de l'angle de diffraction (pour un a raisonnable >)
Quand a diminue, augmente, mais une fois que la diffraction a envahi tout l'espace =/2 (première image) et on ne peut pas faire plus (les plaques s'y opposent).
Le texte demande en effet "calculer l'écart angulaire θ, puis déduire l'angle de diffraction."
Je ne peux répondre à aucune des deux questions
- je peux donner mais pas vraiment le calculer
- je ne peux en déduire l'angle de diffraction, parce que je ne connais pas la distinction que vous avez faite dans le cours entre ces deux grandeurs.
(Peut-être que l'angle de diffraction, c'est le demi-angle d'ouverture donc /2 et l'écart angulaire l'angle total donc ).
Combien de fois faudra-il dire que =/a n'est correcte qu'aux petits angles, que 143° n'est pas petit et que de tout manière (si c'est le demi-angle) ne peut dépasser 90°.
La "formule" pour les angles quelconques est qui n'est a priori pas au programme de terminale. Mais même celle-là ne convient pas : cela donne
plutôt problématique. (Je viens de m'apercevoir de votre erreur numérique : 5/2=2,5 et non 2,2).
Donc je ne sais toujours pas " calculer l'écart angulaire θ " ou alors il y a qqch qui m'échappe.
Bonsoir
Merci beaucoup de m'avoir répondu !
Effectivement c'est 2,5 rad !
donne un valeur très petit
NON !
Cela n'a pas de solution, le sinus est toujours inférieur à 1.
Oui effectivement le sinus est entre
-1≤sin x≤1 , en intéressant pour sin x≤1
Pourquoi n'a pas de solution
Merci beaucoup
Cela sort, nettement, du cadre de la Terminale : l'angle de diffraction correspond à la direction dans laquelle l'intensité I est nulle, il se trouve simplement que I est non nulle en tout point.
Annuler
connectez vous