Bonsoir,

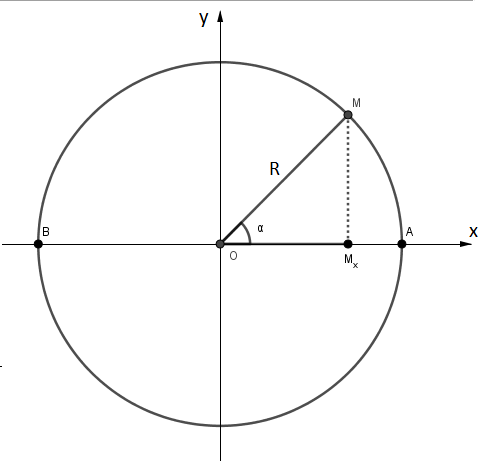
Imagine un cercle de rayon R sur lequel se trouve un point M
Soit M_x la projection de M sur l'axe Ox

1) Peux tu exprimer l'abscisse x du point M_x en fonction de R et de α ?

Imagine qu'à partir de maintenant le point M tourne indéfiniment sur le cercle avec une vitesse angulaire constante ω
2) Quelle sera alors la trajectoire du point M_x ?

3) En supposant qu'à la date t=0 le point M se trouve en A peux tu exprimer la mesure de l'angle α en fonction de ω et de t ?

4) Peux tu alors exprimer l'abscisse x(t) du point M_x  en fonction de R, ω et t ?

Bonjour
1) oui l'abscisse de Mx sa sera Rcos(alpha)
2) la trajectoire de Mx sa sera une droite
3) le mouvement est curculaire uniforme donc , alpha(t)=wt + cst
4) d'aprés ce qui precede
X(t)= Rcos(wt + cst)
Mais ici c'est la mouvement de la projection du mobile qui se fait dans une seul axe ,

Un mouvement rectiligne qu'il soit sinusoïdal ou non est un mouvement dont la trajectoire est une droite ( ou un segment de droite )
Pour décrire un tel mouvement un seul axe est suffisant.
Si tu tiens à utiliser un repère tridimensionnel Oxyz un mouvement rectiligne (sinusoïdal ou non) selon l'axe Ox pourra être décrit par :
x(t) = f(t)    
y(t) = constante
z(t) = constante

Par exemple pour un mouvement rectiligne sinusoïdal :
x(t) = X_m cos (t + )
y(t) = 0
z( t) = 0

Donc , c'est la projection du mobile sur (ox) qui effectue un mouvement rectiling sinusoidal et non le mobile?

Rien n'empêche la projection M_x  d'être constitué par un mobile.

C'est ce qui se passe pour le mouvement d'une masse accrochée à un ressort qu'on a étiré puis lâché.
Dans ce cas, seul le point Mx (la masse) est bien réel. Le cercle, le point M et l'angle = t + sont "virtuels"

ok  j'ai compris, dans le cas du ressort Mx=M
Donc c'est le mobile qui effectue un mouvement rectiling sinusoidal
Mais dans le cas où la trajectoire est demi cercle ( le mouvement d'une Balançoire)
c'est M qui effectue un mouvement rectiling sinusoidal où Mx? Merci

Ok, donc c'est Mx , mais je confus un peu , parce que j'ai vu dans beaucoup d'enonces que M c'est celui en mouvement rectiling sinusoidal