Inscription / Connexion Nouveau Sujet
mouvement dune tige
Une barre AB, homogène, de section constante, de masse M = 4kg et de longueur L = 1,4m
est mobile sans frottement au tour d'un axe horizontal situé au voisinage immédiat de son
extrémité A. A l(instant t = 0, La barre est horizontal et son énergie potentielle est nulle, on
communique alors son extrémité B une vitesse V vertical, dirigée vers le bas, de valeur
V = 5m/s.
a. Calculer l'énergie mécanique de la barre au début de son mouvement / On donne
J∆ = 1/3.ML².
b. Quelle est au cour du mouvement, la hauteur maximale atteinte par le pont B ; La
repérer en prenant comme référence le niveau de l'axe.
c. Quelle est la vitesse angulaire w de la barre lorsque le centre d'inertie G passe par
l'altitude zB = -1m ? Pour quelle valeur de zB la vitesse angulaire est - elle
maximale ?
Calculer numériquement wmax correspondante.
d. Quelle valeur minimale Vmin faut-il donner à la vitesse initiale du point B pour que la
barre fasse le tour complet de l'axe.
e. On lance désormais la barre à partir de la même position horizontale, mais en
imprimant au point B une vitesse verticale V dirigée vers le haut de valeur V' =
10m/s. Quelles sont les vitesses V1 et V2 du point B lorsqu'il passe à la verticale,
respectivement, au dessus de l'axe puis au dessous ?
Hello (c'est tjrs mieux avec un petit bonjour pour commencer)
A la question b/ tu as déterminé une hauteur maximale (appelons la zmax) atteinte par le point B. cette hauteur était fonction de V (vitesse initiale de B)
si zmax < L la barre ne fera pas un tour complet
Il existe donc une vitesse "critique" pour laquelle zmax = L. Et pour toute vitesse de lancement supérieure à cette vitesse critique, la barre fera un tour complet.
A toi?
cest vrai avant de parler un petit bjr cest mieux EXCUSE alors jai dit que jai un probleme de demarrage pour cette exercice
je croyais avoir lu que c'était la question d qui te posait problème
a) énergie mécanique au début du mouvement:
C'est la somme de l'énergie potentielle de pesanteur et de l'énergie cinétique
On te dit dans l'énoncé que l'on choisit la position horizontale de la barre comme position où l'énergie potentielle est nulle donc
On te dit également que
Par ailleurs on dit que le point B est lancé avec une vitesse V, donc au lancement, la vitesse de rotation de la barre est
Donc
b) hauteur maximale atteinte:
Il n'y a pas de frottements nous dit l'énoncé, donc l'énergie mécanique se conserve
Si la barre est lancée avec une vitesse initiale suffisamment importante, elle va faire des tours complets et
Si la barre ne fait pas de tours complets (pas lancée suffisamment "fort") alors B atteint une altitude comprise entre 0 et L
Et en ce point sa vitesse est nulle, donc son énergie cinétique également:
donc
Te voilà remis en selle?
mais si cest le cas contraire cest a dire la barre est pendu suivant laxe vertical la vitesse quil faut exercice sur lextremite B pour que la barre fasse un tour complet je vois pour le travail du poids la hauteur au sommet de sa trajectoire est ecrite sur cette forme L/2+L/2cosa différente de ce cas la je veux savoir comment déterminer cette hauteur cest ça mon problème
Pas de souci. N'hésite pas à rapporter ici tes résultats afin que nous puissions t'aider si besoin. A+
pour la question b en appliquant la conservation de Energie mécanique jai trouver mgZmax=1/6 x mVcarre alors Zmax=1/6g x V carre et pour la question b on peut passer per le theoreme de Em en posant zB = -1m dans ce cas
Attention:
Pour la question b/ l'énergie potentielle de la barre ne vaut pas mais
En effet la résultante du poids de la barre s'applique à son centre de gravité (appelons le G) et
Donc à l'altitude maximale:
Soit
Cette remarque vaut également lorsque tu exprimes la conservation de l'énergie mécanique en
C'est bon?
oui et en zB = -1m on a -mg/2+1/6 x mvBcarre=1/6 x mVcarre et avec vB je peut determiner wB et pour le suivant svp
Je reformule par sécurité 
A un instant où le point B est à l'altitude z animé d'une vitesse angulaire
Le conservation de l'énergie mécanique fournit:
Donc, comme \
Soit
Cela te permet au passage de trouver le résultat de b/ (en résolvant v_B = 0)
Pour
est décroissante sur l'intervalle
Comme on s'en doute la vitesse est maximale (énergie cinétique maximale) lorsque l'altitude est minimale (énergie potentielle minimale), l'énergie mécanique étant pour sa part constante. Donc pour
On a alors
mon probleme avec cet exercice cest la comprenhension de ce phenomene de rotation la prise des altitudes positif et negative jai meme tenter de faire lexperience pour comprendre le mecanisme et pourquoi Z est egale a la moitie de zB si Z est prise comme reference sur laxe tout ces truc la vraiment je veux vraiment comprendre
Pas certain d'identifier, à la lecture de ton dernier message (un peu flou), ce qui te pose souci.
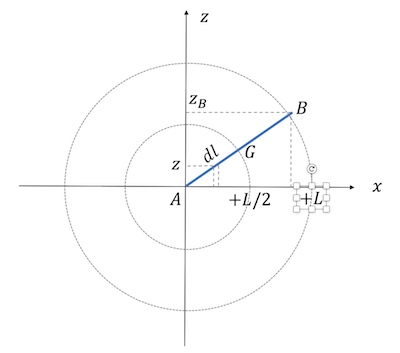
Jette un oeil au schéma ci dessous.
1er constat: la valeur de l'énergie potentielle est entièrement déterminée par la donnée de :
en effet, l'énoncé règle la question de "à une constante près" en fixant pour
Et par ailleurs, on se représente bien que
Ensuite, le système étudié, étant la barre, déterminons l'énergie potentielle de la barre:
methode A (je connais mon cours): le centre de gravité G étant par définition le point d'application des forces de pesanteurs qui s'exercent sur la barre:
Or G est le milieu de [AB], la barre étant homogène: donc
Donc
methode B (je me méfie de mon cours  )
)
l'énergie potentielle est la somme des énergies potentielles des portions élémentaires de barre comprises en A et B
Donc
Ouf on trouve le même résultat (d'où l'intérêt de connaitre les fondamentaux du cours ...)
Est ce plus clair?
au dessus de laxe verticale zB = L/2 et au dessous zB = -L/2

Au dessus zB = +L au dessous zB = -L
(c'est le centre de gravité G qui tourne sur un cercle de rayon L/2)
Je complète le schéma que de tte façon je n'avais pas joint à mon dernier message
En espérant que cela éclaircisse tout ce qui doit encore l'être