Inscription / Connexion Nouveau Sujet
Mouvement du centre d'inertie
Bonjour,
Aidez moi svp à corriger cet exercice.
Problème
Dans toute cette étude d'un saut de ski, on négligera les frottements de l'air sur le skieur bien qu'en réalité ce dernier utilise la résistance de l'air lors de la phase aérienne. Un sauteur à ski, de masse m = 75 kg s'élance sur un tremplin dont la piste de longueur 150 m est située entre l'altitude 1540 m et l'altitude 1440 m. Ce tremplin se termine par une partie horizontale.
1) quelle est la valeur de la vitesse du skieur quand il quitte le tremplin en O, sachant que les frottements de la neige sur les skis sont équivalants à une force de valeur constante et égale à 400 N ? On prendra g = 10 SI.
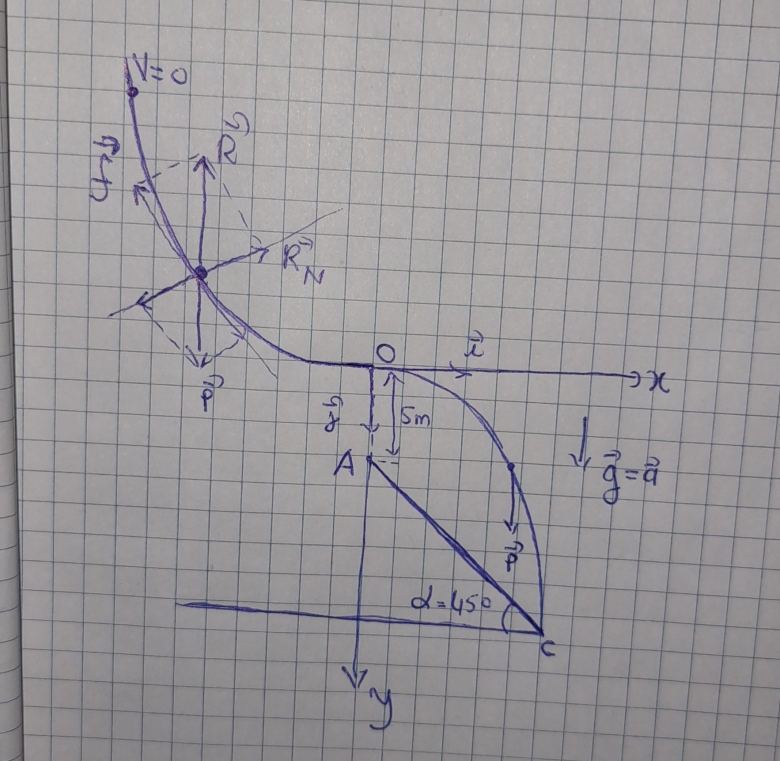
2) La piste d'atterrissage est plane et inclinée à 45⁰ par rapport à l'horizontale. Elle passe par un point A situé sur la verticale du point O, à 5 m en-dessous de ce dernier.
Déterminer à quelle distance du point A le skieur touche le sol.
Bonjour,
Tu n'es pas un nouveau membre, pour initier un échange il faut que tu détailles ce que tu as été en mesure de faire ; sans cela, pas d'échange constructif qui vaille : système, référentiel, bilan des forces, schéma de la situation, théorèmes ou loi utilisées, justifications, hypothèses, ...
D'accord,
Pour la 1ère question :
- système étudié : skieur de masse m
- référentiel terrestre supposé galiléen
- bilan des forces : le poids P du skieur et la la réaction R de la piste sur le skieur.
Le Théorème de le l'Ec entre le point de départ et le point d'arrivée O donne, sachant qu'à t = 0, la vitesse est nulle :
½mV02 = WP + WR
Où WP=mgh (où h = 1540-1440=100 m)
Et WR= - f*l ( où l est la long du trajet)
Enfin, le TEc devient :
V02 = 2gh - 2f*l/m
AN : V02 = 400
Soit V0 = 20 m/s
C'est au niveau de la 2ème question que j'ai des difficultés. Selon mon schéma, je dois calculé la distance AC. J'avoue que je n'arrive même pas à commencer
Bonjour,
Oui, ton schéma est correct.
1. OK pour ta proposition
2. Cette partie correspond à l'étude d'un projectile soumis à un gens de pesanteur : tu as donc un système uniquement soumis à son propre poids, tu peux donc appliquer la deuxième loi de Newton.
Je ne vais pas être disponible toute la journée, si quelqu'un veut prendre la relève ...

bonjour,
2) on néglige la résistance de l'air, donc le mouvement entre O et C est une chute libre avec vitesse initiale : c'est une application directe du cours.
Il faut déterminer les équations horaires, puis l'équation de la trajectoire et chercher les coordonnées de C qui est l'intersection entre la branche de parabole et la droite (AC) et enfin calculer AC (on connait les coordonnées de A).
D'accord
Entre O et C, le skieur n'est soumis qu'à la seule action de son poids (la résistance de l'air est négligée). Donc la chute est libre, avec un vecteur vitesse initiale parallèle à l'axe Ox.
Le Théorème du centre d'inertie donne :
P(vecteur) = m*a(vecteur)
Soit a(vecteur)=g(vecteur)
Sois un repère R(XOY) tel que Ox parallèle à Vo et Oy un axe vertical descendant.
Les coordonnées du vecteur accélération sont :
ax=0 et ay=g
Les coordonnées du vecteur sont :
Vx=V0=constante et Vy=gt (car V0y=0)
Les coordonnées du vecteur position sont :
x = V0t et y = ½gt² (car à l'instant initial x0=y0=0)
En éliminant t entre x et y, j'obtiens l'équation de la trajectoire : y = g*x²/(2*V0²).
Est-ce vrai jusque là ?
Oui
on obtient la trajectoire: y = , avec x>0
qui est une branche de parabole
Autre point: sur le schema, et
ne sont pas colineaires
Merci pour la précision.
Maintenant, l'équation de la droite (AC) :
Je pose : y = x*tan45⁰ - AO
Sois y = x - 5
Or en C, la droite (AC) coupe la parabole. Donc on pose : yc=xc-5
Et d'autre part : yc=g*xc²/(2V0²)
Par la suite : yc=yc, on obtient, en remplaçant g et V0 :
xc-5=0,0125xc²
Puis je résous cette équation pour trouver xc.
C'est ça ?
Attention à l'orientation de (Oy) dans le repère choisi.
A a pour coordonnées (0,5) et non pas (0, -5) donc l'équation de (AC) est y=...
Sinon c'est la bonne méthode.
Donc l'équation de la droite (AC) est y = x + 5
Au point C, à l'intersection j'obtiens :
x + 5 = 0,0125x²
Soit 1,25x² - 100x - 500 = 0
Je trouve les racines x1 = 84,7 et x2= - 4,27 (à rejeter)
Donc yc=84,7 + 5 = 89,7
En fin, AC² = xc²+yc²
Je trouve AC = 123,7 m
C'est ça ?
Ah d'accord, je vois ! ! !
Donc AC² = xc² + (yc-5)²
AC² = 84,7² + (89,7-5)²
AC² = 2*84,7²
Soit AC = 119,78 m
C'est ça !
Oui
on obtient la trajectoire: y =
qui est une branche de parabole
Autre point: sur le schema,
Comment avez vous fait pour écrire P et R avec les vecteurs dessus ?
En utilisant le Latex qui est un langage permettant d 'ecrire des formules
(Boutons LTX en bas de la fenêtre d'edition)
Il y a aussi un éditeur Latex intégré.
Exemple: \vec{P} = \vec{0} écrit entre les balises Latex donne:
[ tex]\vec{P} = \vec{0} [/tex] ==>