Inscription / Connexion Nouveau Sujet
mouvement de l hélium
Bonjour
Énoncé:
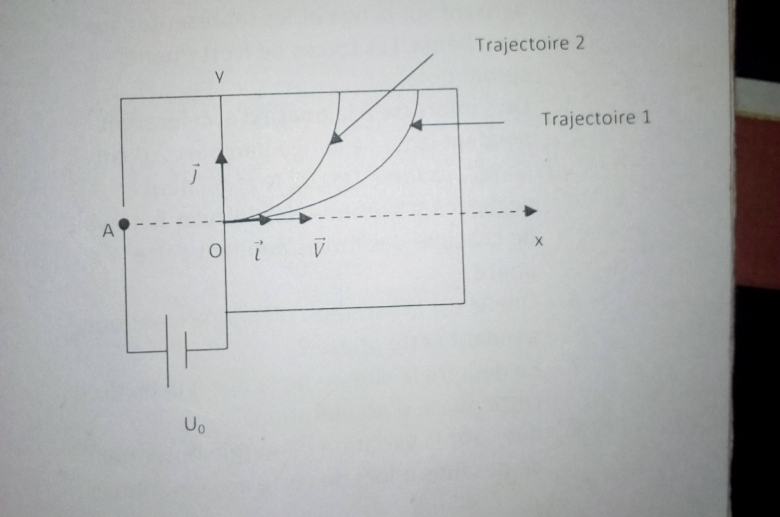
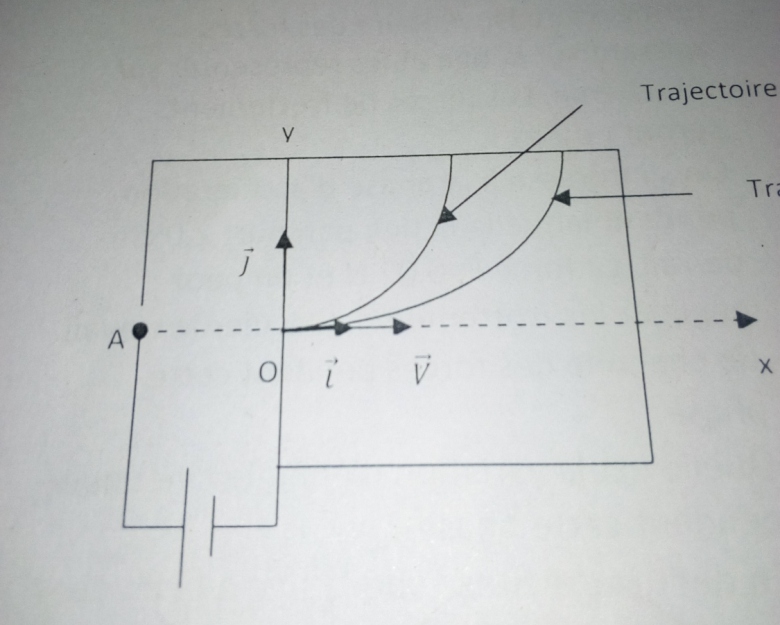
Un noyau d hélium sort d une source s pratiquement sans vitesse par l ouverture A.il est soumis a l action d une tension accélératrice Uo .déterminer sa vitesse VO lorsque il passe par l couverture O .il pénètre dans une région ou régné un champ B(voir schéma)
1/ représenter le champ B, justifier
2/ montre que le mouvement du noyau d hélium est plan ,circulaire et uniforme
3/ en déduire, l expression du rayon en fonction de m,Uo, e et B
4/ identifier la trajectoire sur le schéma
On remplace le champ B par un champ E
5/ représenter le champ E , justifier
6/ déterminer l accélération puis établir l équation de la trajectoire en fonction de E et Uo
7/ identifier la trajectoire sur le schéma
8/ on souhait que le noyau sorte de la région au point s(XS=0,8,ys=0,33)
Déterminer l espace champ qui convient.
Données : e=1,6*10^-19 C, Uo=1000V /m, masse de He^2+ =6,65*10^-10 ^27 kg ,B=0,028 T
Question
Déterminer VO
Application du théorème de l énergie cinétique
∆EC =qUo
Vo= (
()
Vo=2,2*10^5 m/s
Question 1
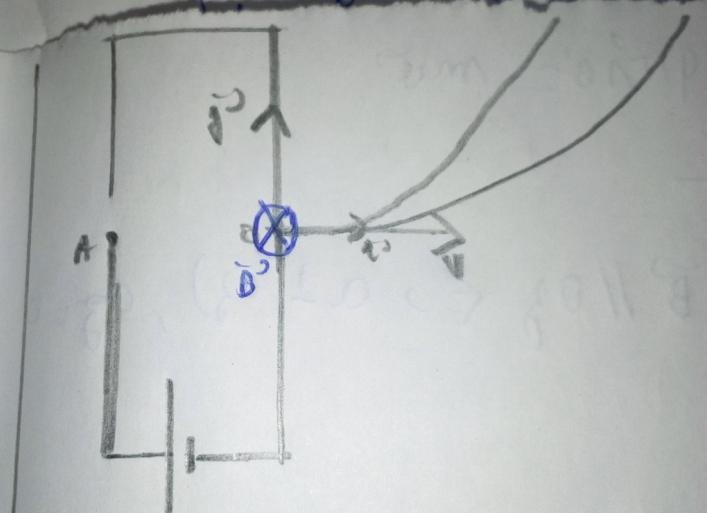
Lorsque l hélium arrive en o ,sa vitesse est orienté de A vers O
Il est orienté vers le haut ,sens de la force
Donc le champ est oriente de ton oeil vers la feuille 
Bonsoir,
Ton schéma est mal cadré, on ne voit pas en entier les indications qui y figurent.
Question 3 :
Attention, un noyau d'Hélium n'est pas un proton, sa charge n'est pas égale à " e "
Bonsoir,
Ton schéma est mal cadré, on ne voit pas en entier les indications qui y figurent.
Question 3 :
Attention, un noyau d'Hélium n'est pas un proton, sa charge n'est pas égale à " e "
Bonjour odbugt1, concernant le cadrage de l'image, c'est de ma faute, j'ai trop rogné le côté droit, voilà qui est corrigé

@gbm
Bonjour et merci gbm, mais bien qu'ayant vidé le cache de mon navigateur l'image est toujours tronquée. Il me manque le texte.
@moussolony
Oui, le champ magnétique est bien orienté comme indiqué dans ton post du 27-01-20 à 18:44
@odbugt1 : le texte était déjà tronqué dans la version initiale de la photo (je viens de vérifier). Ce faisant, je le fais disparaître car c'est à recopier 
Question 6
Application du théorème du centre d inertie
F=ma
a=(qE)/m
Projection dans le repéré (o,i,j)
a=(qE)/m=(qE)/m x{ ax= (qE)/m,ay=0}
ax=(2*2*1,6*10^-19*500)/(6,65*10^-27)
ax=0,48 *10^11 m/s
a t=0, OM{ XO=0, yo=0} v{ vox=VO, voy=0}
OM{x(t)=(qE)/mt^2, y(t)=0}..
Est ce c est correct?
Question 3
R=R=(m
 ((4eUo)/m)/2eB
((4eUo)/m)/2eBOui, ce résultat est exact mais serait plus lisible sous la forme :
Question 6 :
Il serait judicieux de répondre d'abord à la question 5 avant de revoir entièrement cette question et en profiter pour soigner la présentation du calcul.
Et puis :
Les données qui figurent à la dernière ligne de l'énoncé comportent une bizarrerie :
U0 = 1000V/m
Un champ électrique s'exprime en V/m mais pas une tension
ax=(2*2*1,6*10^-19*500)/(6,65*10^-27)
Répondre à la question 5 ne veut pas dire revenir au début de l'exercice dans la phase d'accélération.
Lire l'énoncé :
Il s'agit de représenter le champ après remplacement du champ
par le champ
Non
Dans le champ électrique :
La figure de l'énoncé montre que les noyaux d'Hélium sont déviés vers le haut.
Ils sont donc soumis à une force et un champ vertical dirigé vers le haut.
Dans le champ magnétique:
La force de Lorentz et la vitesse initiale sont coplanaires.
Le mouvement a donc lieu dans le plan auquel ils appartiennent.
Voici ma proposition
Application du théorème du centre d inertie
F=ma
a=(qVB)/m
a perpendiculaire a (B) et B parallèle a (oz) ,az= 0. Et az=ce
z=aozt+zo
aoz perpendiculaire a (B) <=> aoz perpendiculaires (Oz) ,aoz=0
z=zo=cte
Zo=0
Donc le mouvement du noyau d hélium est plan
Question 6
Système : noyau d hélium
Référentiel : terrestre supposée galiléen
Inventaires des forces
Force électrostatique
Application du théorème du centre d inertie
Fe=ma<=> a=(qE)/m
Projection dans le repéré (o.i,j)
a{ ax=0, ay=(qE)/m}
ay=(2eE)/m
ay=0,4812 m/s^2
Question 6
Projection dans le repéré (o,i,j)
a t=0, OM{ XO =0 , y=0} , v{ vox=VO, voy=0}
OM{ x(t)=vot, y(t)=(2eE)/m t^2}
y=
y=
y=
Question 6 :
J'ai trouvé :
En éliminant " t " entre " x " et "y" on obtient :
Et en remplaçant
Question 7
C est la trajectoire 2
Comment justifier cela?
Que proposes tu ?
D après l équation de la trajectoire trouvé ,on constat que la trajectoire est parabolique
La trajectoire 2 n est pas parabolique .
Donc la bonne réponse c est la trajectoire 1
Question 8:
Je ne comprends pas cette question.
Qu'est ce que l'espace champ dont il est question ici ?
Pourquoi calcules tu la valeur de E puisque d'après toi l'énoncé donne cette valeur ?
Voir à ce sujet ton post du 28-01-20 à 23:08