Bonsoir
Au cours d une compétition de tennis, deux joueurs A et B s affrontent. Le joueur A voyant son adversaire avancer, décidé de le lober.
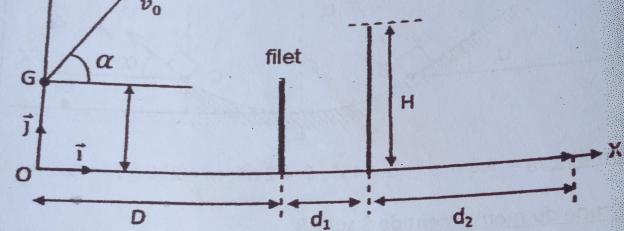
Le centre d inertie G de la balle de masse m est a une hauteur h=0,5m du sol et le filet a une distance D=12 m du point O
Le joueur A frappe la balle avec sa raquette a la date =0.celle ci part avec un vecteur vitesse VO faisant un angle a=60° avec l horizontale.l action de l air. Est négligée.
On donne VO=14 m/s et g=9,8 m/s^2

1/déterminer dans le repéré (0,i,j)
1.1.1.les équations horaires x(t), y(t) du mouvement de G en fonction de g, VO, a,h et t.
1/2.l équation cartésienne de la trajectoire du centre d inertie G de la balle
1/3 .vérifier que cette équation s écrit:
y=-0,10x^2+1,73x+0,50

2/le joueur B, se trouvant a une distance d1=2 m  derrière le filet tente d arrêter la balle en levant verticalement sa raquette ,a une hauteur H=3 m.
Montrer que le joueur ne peut intercepter la balle.
3/la balle tombe en un point c situé sur l axe OX.calculer la distance OC.

4/la distance séparant le joueur B et la ligne de fond est d1=10 m.
4/1.la balle tombe t elle dans la surface de jeu?
4/2determiner
4/2.1la vitesse avec laquelle la balle arrive au point C.
4/2/2.le temps mis par la balle pour atteindre le point C.


Réponse
Question 1/1
Système : la balle de masse m
Référentiel : terrestre supposé galiléen.
Inventaires des forces:
Le poids p de la balle
Application du théorème du centre d inertie
P=ma
a=g=cte.
A t=0, OMo{XO=0,yo=h} et VO{ vox=VO*cosa, voy=VO*sina}

a t#0,application du théorème du centre d inertie.
a=g=-gj.a{ax=0,ay=-g}

OM{x(t)=VO*cosat, y(t)=-g/2*t^2+VO*sinat+h

Question 1/2
y=-g/(2*V^20*cos^2a)+xtana+h

Question 1/3
y=-9,8/2*14^2*cos^2(60)+xtan(60)+0,5
y=-0,1x^2+1,73x+0,5

Question 2
y=-0,10*(14)^2+1,73*14+0,5
y=5,12
y>H.donc le joueur ne peut intercepter la balle.

Question 4

La balle est tombe.donc y=0
-0,10x^2+1,73x+0,50=0
∆=1,73-4*-0,10*0,50
∆=1,93
∆=1,389.
X1=-1,73-1,389/-0,2
X1=15,6
La distance OC est :15,6 m.

Question 4/1
J ai besoin d aider