Inscription / Connexion Nouveau Sujet
Mouvement d'un solide
Bonsoir . J'ai un exercice que je n'arrive pas a résoudre :
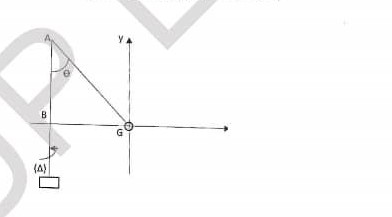
un solide de masse m =500 g est assimilé à son centre d'inertie G. Il est relié aux points A et B par deux fils inextensibles de masses négligeables( voir figure). Les fils sont accrochés à un axe delta vertical, solidaire d'un moteur qui entraine le solide dans un mouvement de rotation, à la vitesse angulaire w constante. Soit T1 la tension du fil AG et T2 celle du fil BG .
Téta est l'angle entre l'axe delta et AG. Lorsque le fil BG est tendu, il est alors perpendiculaire à delta .
La longueur de AG=l=50 cm. La longueur de BG est l'=43,30cm . On donne l'intensité du champ de pésanteur g=10m/s2.
1) Donner la valeur de l'angle Téta lorsque w=0? Déterminer alors la tension T1 du fil
2) la vitesse angulaire du solide w est désormais différent de 0
2.1) En appliquant le Théoreme du centre d'inertie au solide , dans le répere ( G,x,y), établir que
On remarquera les coordonnées du vecteur accélération sont : ax=-an et ay=0 et le rayon de la trajectoire r=BG.
2.2) En déduire que le solide G ne s'écarte de l'axe , que si w
w0 =
2.3) Déterminer lorsque
, la tension T1 du fil AG.
3) On considére que .
3.1) Pour quelle valeur 
1 de l'angle le fil BG commence à se tendre .
3.2) Calculer la vitesse angulaire w1 du solide si =1 ; le fil BG étant toujours considéré non tendu
II- ETUDE DU SYSTEME LORSQUE LE FIL BG EST TENDU
La vitesse angulaire w du solide est telle que
1) Quelle est la valeur de l'angle ?
2) Déterminer les tensions T1 et T2 des fils lorsque w=10rad/s
Merci de m'aider.
Pour la première question puisque w=0 alors le solide est en équilibre donc en appliquant le principe d'inertie je pourrai déterminer T1 mon soucis est au niveau de l'angle téta
donc mais comment trouver l'expression de cos() parce que lorsque je projette sur l'axe (Gx) d'apres le TCI j'obtiens : T1sin()=-man. Donc mgsin()=-man alors sin() =
0 et T1 Sur (Gy) : T1cos()-P=0 (1)
Sur (Gx) : T1sin()=-ml'w2 (2).
Si je remplace T1=
dans (2) il y a tangente qui apparait...
2.1) ici BG = r < l' (donc un seul fil tendu)
T1= mg/cos
- T1sin = - m r w2
Et comme r = l sin , sin se simplifie et on trouve le résultat attendu
cos 
(l/g)mais ici on demande 1 a partir du quel le fil se tend donc il faut que lsin()=l' c'est a dire sin()=
mais dans la question suivante il est dit que le fil n'est pas tendu mais de calculer w1 lorsque Téta 1 = Téta
Oui, on est juste à la limite de la tension du fil BG, donc on peut encore appliquer la formule de la question 2)
Le triangle est toujours rectangle sinon on ne pourrait pas ecrire r = l sin
Si w > w1, BG ne change pas de longueur puisque le fil tendu l'en empeche donc =...
Annuler
connectez vous