Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau terminale
Partager :

Mouvement d'un proton dans un champ électrique uniforme

Posté par
blenderiste09 12-12-13 à 16:23

Bonjour,
J'ai un exercice de physique dans lequel on me demande de calculer la trajectoire d'un proton plongé dans un champ électrique uniforme.

Voiçi l'énoncé:

On considère le movement d'un proton de masse m et de charge +e qqui entre en H avec une vitesse v_0 dans une région de l'espace où règne un champ électrique uniforme E orienté suivant l'axe Oz.

On suppose que le mouvement a lieu dans le plan xOz, avec Oz axe vertical dirigé vers le haut et Ox: axe horizontal de même direction que (voir figure ci-dessous).

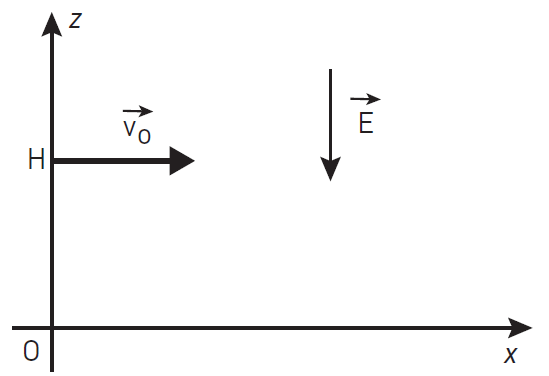
Mouvement d\'un proton dans un champ électrique uniforme



Donnée: m = 1,67.10^{-27} kg; e = 1,6.10^{-19} C; E = 790 V.m^{-1}; OH = 1,0 m.

1) Déterminer les coordonnées a_x et a_z du vecteur accélération.

Pour faire court, j'ai montré que le poids de la particule était négligeable devant la force électromagnétique.

Donc, d'après la seconde loi de Newton:
\vec a = q \vec E

Donc:
a_x = 0
a_z = 1,6.10^{-19} × 790 = 1,2.10^{-16}
Or \vec E est colinéaire à Oz et dirigé vers le bas.
Donc a_z = -1,2.10^{-16}


2) En déduire les coordonnées de la vitesse.

Içi j'ai intégré l'accélération par rapport au temps.
J'obtient donc la vitesse du proton.
Soit:
v_x = v_0 × cos
v_z = q × E × t + v_0 × sin


3) En déduire les équation horaires du mouvement.

J'ai intégré les coordonnée de la vitesse par rapport au temps et j'ai obtenu les coordonnée du vecteur position.
Soit:
x(t) = v_0 × cos × t
z(t) = \frac{1}{2} q × E × t^2 + v_0 × sin × t + 1

Or, l'angle = 0°, donc sin = 0 et cos = 1.

Donc:
x(t) = v_0 × t
z(t) = \frac{qE}{2}t^2 + 1

4) Trouver l'équation de la trajectoire z(x).

x(t) = v_0 × t
Donc t = \frac{x}{v_0}

Je remplace l'expression de t dans l'équation horaire z(t) obtenue précédemment.

On obtient donc z(x) = \frac{qE}{2 v_0^2}x^2 + 1

5) Quelle est la nature de cette trajectoire ?

La nature de cette trajectoire est une parabole.

6) Calculer la durée nécessaire pour que le proton atteigne l'axe x.

C'est içi que je n'arrive pas.

Il me manque v_0.
Est-ce que j'ai fait une erreur ?


Pouvez-vous m'aider ?

Merci d'avance.


Blenderiste09

Posté par
Coll Moderateurre : Mouvement d'un proton dans un champ électrique uniforme 12-12-13 à 17:02

Bonjour,

Le vecteur accélération doit être déduit de la seconde loi de Newton.
Mais ce n'est pas ce que tu as fait.

Peux-tu écrire la seconde loi de Newton en toutes lettres (dans une phrase) et non pas dans une "formule". Tu te rendras vite compte de ton erreur.

Posté par
J-Pre : Mouvement d'un proton dans un champ électrique uniforme 12-12-13 à 17:16

(en vecteurs)
F = q.E (et F = m.a) --->
a = q.E/m

ax = 0
az = 1,6.10^-19 * (-790/(1,67.10^-27)) = -7,57.10^10 m/s²
---
vx(t) = Vo
vz(t) = -7,57.10^10.t
---
x(t) = Vo.t
z(t) = OH - 7,57.10^10.t²/2 = 1 - 3,78.10^10.t²
---

t = x/Vo
z = 1 - 3,78.10^10.x²/Vo² (arv de parabole)
-----
Atteint l'axe des x à l'instant t1 tel que 1 - 3,78.10^10.t1² = 0
t1 = 5,14.10^-6 s

Sauf distraction.  

Posté par
J-Pre : Mouvement d'un proton dans un champ électrique uniforme 12-12-13 à 17:16

Oups ....

Salut Coll.  

Posté par
blenderiste09re : Mouvement d'un proton dans un champ électrique uniforme 12-12-13 à 17:19

Bonjour,

Merci pour ta réponse.

Dans mon cours, il est dit: "Dans référenciel galiléen, la somme des forces extérieures exercée sur un système est égale à la dérivée par rapport au temps de la quantité de mouvement"


Mais je ne comprend toujours pas.

Merci encore.

Blenderiste09

Posté par
Coll Moderateurre : Mouvement d'un proton dans un champ électrique uniforme 12-12-13 à 17:23

Bonjour J-P

Aucun problème !
____________________

blenderiste09 >>
Oui. Et à quoi est égale la quantité de mouvement ?

Posté par
blenderiste09re : Mouvement d'un proton dans un champ électrique uniforme 12-12-13 à 17:31

A la somme des forces extérieure exercées sur le système, içi la force électromagnétique.

Posté par
Coll Moderateurre : Mouvement d'un proton dans un champ électrique uniforme 12-12-13 à 17:43

Ah non, pas du tout.

Posté par
blenderiste09re : Mouvement d'un proton dans un champ électrique uniforme 12-12-13 à 17:55

Ben, pourquoi ?

Posté par
Coll Moderateurre : Mouvement d'un proton dans un champ électrique uniforme 12-12-13 à 17:57

Quelle est la définition de la quantité de mouvement d'un mobile ?

Posté par
blenderiste09re : Mouvement d'un proton dans un champ électrique uniforme 12-12-13 à 18:00

p = m×v

Posté par
Coll Moderateurre : Mouvement d'un proton dans un champ électrique uniforme 12-12-13 à 18:11

Oui !

Je pense que tu as ce qu'il te faut maintenant pour revoir et corriger l'expression de l'accélération que tu as indiquée
 

Citation :
\vec a = q \vec E


expression qui est fausse.

Posté par
blenderiste09re : Mouvement d'un proton dans un champ électrique uniforme 12-12-13 à 18:33

Est-ce que s'est juste ?:
\vec F = m \vec a <=> \vec a = \frac{\vec F}{m}
Or, la masse de la particule est négligeable.
Donc \vec a = \vec F

Par conséquent, \vec a = \vec E et pusique \vec E est dirigé vers le bas, \vec a = - \vec E

Posté par
Coll Moderateurre : Mouvement d'un proton dans un champ électrique uniforme 12-12-13 à 18:56

Non, c'est faux.

Tu étudies en terminale l'analyse dimensionnelle. Elle doit t'éviter d'écrire de telles choses. Et même si tu n'as pas encore "formellement" étudié l'analyse dimensionnelle, je suppose que tes professeurs de physique depuis des années te font porter la plus grande attention aux unités.

Une force ne peut pas être égale à une accélération.

\vec{F}\,=\,m.\vec{a}
(expression la plus courante de la seconde loi de Newton, même s'il est vrai que Newton l'avait formulée en terme de quantité de mouvement)

Dans le champ électrique : \vec{F}\,=\,q.\vec{E}
C'est à ce moment que tu peux t'intéresser à la "masse négligeable". "Négligeable" par rapport à quoi ? Négligeable en cela que le poids de la particule (que tu sais déduire de la masse) sera, ou non, négligeable devant la force électrostatique.
donc
\large \vec{a}\,=\,\frac{q}{m}.\vec{E}

Posté par
blenderiste09re : Mouvement d'un proton dans un champ électrique uniforme 12-12-13 à 19:07

Tu veux dire que la masse de la particule n'est pas négligeable devant force électromagnétique ?

Posté par
Coll Moderateurre : Mouvement d'un proton dans un champ électrique uniforme 12-12-13 à 19:14

On ne peut pas comparer une masse (une grandeur scalaire, en kilogramme) avec une force (une grandeur vectorielle, dont l'intensité est mesurée en newton).

J'ai écrit que si tu veux prouver que quelque chose est négligeable, il faut comparer le poids de la particule et la force électrostatique.

Posté par
blenderiste09re : Mouvement d'un proton dans un champ électrique uniforme 13-12-13 à 09:45

Bonjour,

A partir de quand peut considérer que le poids est négligeable devant une force ?

Posté par
Coll Moderateurre : Mouvement d'un proton dans un champ électrique uniforme 13-12-13 à 10:55

1) Tu calcules les intensités de ces deux forces
2) Tu fais leur rapport
3) Tu dis ce que tu en penses...

Posté par
blenderiste09re : Mouvement d'un proton dans un champ électrique uniforme 13-12-13 à 11:09

\vec P = m × \vec g[tex] \\ [tex]P = 1,67.10^{-27} × 9.8
P = 1,67.10^{-26} N

Je sais que F = 790 N

D'où:
\frac{F}{P} = \frac{1,6.10^{-26}}{790} \\ [tex]\frac{F}{P} = 5.10^{28}

Personnellement, je trouve que cela fait beaucoup. J'en conclu donc que l'intensité du poids de la particule est négligeable devant la force électrostatique.

Est-ce bon ?

Posté par
blenderiste09re : Mouvement d'un proton dans un champ électrique uniforme 13-12-13 à 11:11

\vec P = m × \vec g
P = 1,67.10^{-27} × 9.8
P = 1,67.10^{-26} N

Je sais que F = 790 N

D'où:
\frac{F}{P} = \frac{1,6.10^{-26}}{790}
\frac{F}{P} = 5.10^{28}

Personnellement, je trouve que cela fait beaucoup. J'en conclu donc que l'intensité du poids de la particule est négligeable devant la force électrostatique.

Est-ce bon ?

Posté par
Coll Moderateurre : Mouvement d'un proton dans un champ électrique uniforme 13-12-13 à 11:31

L'arrondi pour l'intensité du poids n'est pas bon :

\vec P = m × \vec g
P = 1,67.10^{-27} × 9.8
P = 1,64.10^{-26} N

Quant à l'intensité de la force électrostatique, ce n'est pas du tout cela. Comment as-tu trouvé cette valeur ?

Posté par
blenderiste09re : Mouvement d'un proton dans un champ électrique uniforme 13-12-13 à 11:45

Mince tu as raison. Je me suis trompé dans la force électrostatique.

Je recommence:

\vec F = q \vec E
Je sais que \vec E = 790 V.m^{-1}
Donc F = 1,67.10^{-19} × 790 <=> F = 1,3.10^{-76} N

Je calcule le rapport:

\frac{F}{P} = \frac{1,3.10^{-76}{1,64.10^{-26}} <=> \frac{F}{P} = 8.10^{-51}

Le rapport étant très petit, le poids n'est pas négligeable devant la force électromagnétique.

Est-ce que c'est bon ?

Posté par
blenderiste09re : Mouvement d'un proton dans un champ électrique uniforme 13-12-13 à 11:47

(J'ai encore fait une erreur dans le LaTeX)

Mince tu as raison. Je me suis trompé dans la force électrostatique.

Je recommence:

\vec F = q \vec E
Je sais que \vec E = 790 V.m^{-1}
Donc F = 1,67.10^{-19} × 790 <=> F = 1,3.10^{-76} N

Je calcule le rapport:

\frac{F}{P} = \frac{1,3.10^{-76}}{1,64.10^{-26}} <=> \frac{F}{P} = 8.10^{-51}

Le rapport étant très petit, le poids n'est pas négligeable devant la force électromagnétique.

Est-ce que c'est bon ?

Posté par
Coll Moderateurre : Mouvement d'un proton dans un champ électrique uniforme 13-12-13 à 11:53

Je te conseille de relire avant de poster en faisant "Aperçu".
Cela est très utile (on voit mieux ses erreurs ainsi) de manière générale et tout particulièrement si l'on utilise le \LaTeX
________

\vec F = q \vec E
Je sais que
. ||\vec{E}|| = 790\;\rm{V.m^{-1}}
. et que q = +e = 1,6.10-19 C
Donc F = ...

Posté par
blenderiste09re : Mouvement d'un proton dans un champ électrique uniforme 13-12-13 à 12:03

Donc F = 1,67.10^{-19} × 790
F = 1,3.10^{-16} N (oups )

D'où:

\frac{F}{P} = \frac{1,3.10^{-16}}{1,64.10^{-26}}

\frac{F}{P} = 7,9.10^9

Le rapport étant important, le poids est négligeable devant la force électrostatique.

En espérant ne pas avoir fait d'erreur de calcul cette fois-çi.

Posté par
Coll Moderateurre : Mouvement d'un proton dans un champ électrique uniforme 13-12-13 à 12:15

La charge du proton n'est pas 1,67.10-19 coulomb mais est d'environ 1,6.10-19 C
__________

Alors...

Rapport des intensités du poids et de la force électrostatique :

\Large \frac{||\vec{P}||}{||\vec{F}||}\;=\;\frac{1,67.10^{-27}\,\times\,9,8}{1,6.10^{-19}\,\times\,790}\; \approx\;1,3.10^{-10}

On a donc toutes les raisons de négliger le poids par rapport à la force électrostatique.

Posté par
blenderiste09re : Mouvement d'un proton dans un champ électrique uniforme 13-12-13 à 12:21

Merci encore pour tes réponses.
Mais je ne comprend toujours pas mon erreur...

Posté par
Coll Moderateurre : Mouvement d'un proton dans un champ électrique uniforme 13-12-13 à 13:37

Pour appliquer la seconde loi de Newton, ou principe fondamental de la dynamique, tu dois écrire :

\vec{F}\,=\,m.\vec{a}

Le mobile de masse m prendra une accélération \vec{a} sous l'effet de la résultante \vec{F} de toutes les forces qui lui sont appliquées.

Il faut donc :
. choisir un référentiel
. s'y doter d'un repère
. faire le bilan des forces appliquées au mobile

Ici, on pense que les deux forces appliquées au mobile de masse m sont :
. son poids \vec{P}
. la force électrostatique \vec{F_e} à partir du moment où il pénètre dans la région où règne le champ électrique

Donc, pour trouver son accélération il faudrait écrire :

\large \vec{a}\,=\,\frac{\vec{F}}{m}

Avec \vec{F}\;=\;\vec{P}\,+\,\vec{F_e}

Mais, le poids étant négligeable par rapport à la force électrostatique, il suffit de considérer :

\large \vec{a}\,=\,\frac{\vec{F_e}}{m}\,=\,\frac{q}{m}.\vec{E}

Posté par
blenderiste09re : Mouvement d'un proton dans un champ électrique uniforme 13-12-13 à 13:51

Ahhh... je commence à comprendre.
Je vais essayer de faire l'exercice avec ce que tu m'as expliqué.

Merci encore.

Posté par
blenderiste09re : Mouvement d'un proton dans un champ électrique uniforme 17-12-13 à 12:33

Bonjour,
Voila ce que j'ai fait:

1) Déterminer le coordonnées ax et az du vecteur accélération.
\vec F = m × \vec a <=> \vec a = \frac{\vec F}{m}
\vec F étant la somme de toutes les forces éxercées sur le proton.
Donc \vec F = \vec P + \vec F_e.
Puisque le poids est négligeable, \vec F = \vec F_e
\vec F_e = q \vec E
D'où:
\vec a = \frac{q}{m}×\vec E

a_x = 0
a_z = \frac{1,6.10^{-19}}{1,67.10^{-27}}×790

a_x = 0
a_z = 7,5.10^{10}

2) En déduire les coordonnées de la vitesse.

v_x = v_0 × cos
v_z = \frac{q}{m}×E×t+v_0×sin

3) En déduire les équation horaires du mouvement.

x(t) = v_0 × cos×t + x_0
x(t) = v_0 × cos×t
z(t) = \frac{1}{2}×\frac{q}{m}×E×t^2 + v_0 × sin×t+z_0
z(t) = \frac{1}{2}×\frac{q}{m}×E×t^2 + v_0 × sin×t+1
Or = 0° donc cos = 1 et sin = 0.
Donc:
x(t) = v_0 × t
z(t) = \frac{1}{2}×\frac{q}{m}×E×t^2+1

4) Trouver l'équation de la trajectoire z(x).

x(t) = v_0 × t <=> t = \frac{x}{v_0}
D'où
z(x) = \frac{1}{2}×\frac{q}{m}×E×(\frac{x}{v_0})^2 + 1
z(x) = \frac{qE}{2m}×\frac{x^2}{v_0}+1
z(x) = \frac{qE}{2m v_0}x^2 + 1

5) Quelle est la nature de cette trajectoire.

La trajectoire est une partie d'une parabole.

6) Calculer la durée nécéssaire pour que le proton atteigne l'axe x.

z(t) = 0
\frac{1}{2}×\frac{1,6.10^{-19}}{1,67.10^{-27}}× 790 × t^2 + 1 = 0
3,7.10^{10} t^2 + 1 = 0
Cette équation est une équation du second degré.
Donc:
= 0^2 - 4 × 3,7.10^{10} × 1
= -1,48.10^{11}
Donc < 0.
Par conséquent, l'équation n'a pas de solution.
Donc le proton n'atteindra jamais Ox.

Je pense que j'ai encore fait une erreur, mais je vois pas laquelle.

Posté par
Coll Moderateurre : Mouvement d'un proton dans un champ électrique uniforme 17-12-13 à 13:34

L'axe des cotes (Oz) est dirigé vers le haut.
Le champ électrique est dirigé vers le bas. La force qui s'exerce sur le proton est donc dirigée vers le bas et en conséquence l'accélération du proton est elle aussi dirigée vers le bas.

Conclusion :
. les coordonnées du champ électrique sont :
\vec{E}\ \begin{array}{|c} E_x\,=\,0\\E_z\,=\,-790\,\ \ (\rm{V.m^{-1}})\end{array}

Les coordonnées de l'accélération sont :
\vec{a}\ \begin{array}{|c} a_x\,=\,0\\a_z\,=\,-7,57.10^{10}\,\ \ (\rm{m.s^{-2}})\end{array}

Celles de la vitesse sont :
\vec{v}\ \begin{array}{|c} v_x\,=\,constante_1\\v_z\,=\,-7,57.10^{10}.t \,+\,constante_2\,\ \ (\rm{m.s^{-1}})\end{array}
et en tenant compte des conditions initiales (donc pour t = 0 s)
\vec{v}\ \begin{array}{|c} v_x\,=\,v_0\\v_z\,=\,-7,57.10^{10}.t\,\ \ (\rm{m.s^{-1}})\end{array}

Celles de la position sont :
\vec{OP}\ \begin{array}{|c} x(t)\,=v_0.t\,+\,constante_3\\z(t)\,=\,-(\frac{1}{2})7,57.10^{10}.t^2 \,+\,constante_4\,\ \ (\rm{m})\end{array}
et en tenant compte des conditions initiales
\vec{OP}\ \begin{array}{|c} x(t)\,=\,v_0.t\\z(t)\,=\,-3,784.10^{10}.t^2 \,+\,1\,\ \ (\rm{m})\end{array}

L'arc de parabole a pour équation (pour t 0 s et t tmax) :
\large z\,=\,-3,784.10^{10}.\frac{x^2}{v_0^2}\,+\,1

Et tmax est la racine positive de l'équation :
-3,784.10^{10}.t^2 \,+\,1\;=\;0

C'est-à-dire pour tmax 5,14.10-6 s


\large z\,=\,-3,784.10^{10}.\frac{x^2}{v_0^2}\,+\,1

Posté par
blenderiste09re : Mouvement d'un proton dans un champ électrique uniforme 17-12-13 à 15:08

Merci beaucoup. J'ai compris l'exercice ! :)

Je vais pouvoir le renvoyer.

A bientot


Blenderiste09

Posté par
Coll Moderateurre : Mouvement d'un proton dans un champ électrique uniforme 17-12-13 à 17:38

Pour ma part, je t'en prie.
À une prochaine fois !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !