Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau terminale
Partager :

Mouvement d'un projectile dans un champs de pesanteur

Posté par
chacha1995 08-02-21 à 20:13

Bonjour,

j'ai une question sur laquelle je reste bloquée

Une balle est lancée sous un angle de 60°par rapport à l'horizontale. Elle atteint une hauteur maximale de 2m. Que vaut la vitesse initiale ?

3,6
7,2
10,4
14,0 m/s

***Titre changé***

Posté par
diracre : Cinétique 08-02-21 à 20:22

Hello

Il existe plusieurs façon de résoudre ce problème.

Et si tu appliquais la relation fondamentale de la dynamique, puis la projetais sur l'axe verticale, et enfin liais la composante verticale de la vitesse à la hauteur atteinte?

Posté par
chacha1995re : Cinétique 08-02-21 à 20:29

J'étais partie sur V = Vx + Vy

or Vy = 0 car sommet de la parabole

Et Vx = Vo cos A  soit  Vx = 10 cos A

Posté par
chacha1995re : Cinétique 08-02-21 à 20:42

je ne comprends vraiment pas alors que je le retourne dans tout les sens

Posté par
diracre : Cinétique 08-02-21 à 21:21

Je réitère mon conseil: applique la relation fondamentale de la dynamique

Posté par
chacha1995re : Cinétique 08-02-21 à 21:55

F = m a ? je ne vois vraiment pas
je suis en reprise d'études, je n'ai peut être pas encore toutes les bases

Posté par
diracre : Cinétique 08-02-21 à 22:12

On avance...
On va supposé l'axe Oy orienté "vers le haut"
La balle est soumise à son poids

\vec{P} = m.\vec{g} et la RFD te dit:   \Sigma \vec{F} = m\vec{a}

Donc \vec{a} = \vec{g}

Soit en projetant sur les axes

a_x = 0
a_y =-g

On s'intéresse à la projection sur l'axe Oy

v_y = ...      et     y = ...

Posté par
chacha1995re : Cinétique 08-02-21 à 22:19

Oui j'avais le fait que l'accélération est égale à g étant donné que c'est considéré comme une chute libre enfin que dans l'axe y et qu'on est en MRUA avec v (t)= vo + gt

mais je ne comprend pas cette histoire de projection sur les axes ?

Posté par
chacha1995re : Cinétique 08-02-21 à 22:34

En fait moi j'ai
selon x, x(t) = Vo*t + Xo donc 1 m = VocosA*t donc t = 0,1/cosA
et selon y, v(0,1/cosa) = VosinA - g (0,1/cosA)
                                            = 10 * (1,5/AP) - 1/(1/AP)
                                             =15/AP-AP

et AP^2= 1^2 + 1,5^2 soit AP =2,05

Posté par
chacha1995re : Cinétique 08-02-21 à 22:45

Je suis désolée j'ai répondu à un autre exercice sur la même conversation ....
Il faut oubliez tout mes derniers commentaires

Posté par
chacha1995re : Cinétique 08-02-21 à 22:50

Donc pour cet exercice : Une balle est lancée sous un angle de 60°par rapport à l'horizontale. Elle atteint une hauteur maximale de 2m. Que vaut la vitesse initiale ?

J'ai fait hauteur maximale Y = 2 m = Vosin60°*t - (g*t^2)/ 2

et Quand Hauteur max atteinte, V = 0 soit t = Vo / g = Vo/10

Donc 2 = Vo^2 * (Rac3/20)- Vo^2/20g
Soit Vo^2 = 2/((rac2/20)-1))

Posté par
chacha1995Cinématique 08-02-21 à 23:04

Bonjour,
J'ai beaucoup de mal à résoudre cet exercice...

Pouvez vous m'aider ?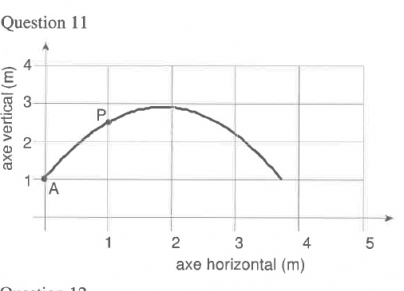

Cinématique

***Image recadrée***

*** message déplacé ***

Posté par
chacha1995re : Cinétique 08-02-21 à 23:06

C'est bon j'ai trouvé le bon résultats mais je pense qu'il y avait bcp plus rapide que ce que j'ai fait ... Car je n'ai pas réussi à utiliser votre méthode
Merci en Tout cas

Posté par
diracre : Cinétique 08-02-21 à 23:30

Donc

v_y = -gt + v_0sin\alpha

y = -\frac{gt^2}{2} +  v_0sin\alpha t

Au point culminant v_y = 0 donc pour  t= \frac{v_0sin\alpha}{g}

Donc, en reportant dans la 2eme équation     h =  \frac{v_0^2sin^2\alpha}{2g}

v_0 = \frac{1}{sin\alpha}\sqrt{2gh}

Posté par
odbugt1re : Cinématique 08-02-21 à 23:31

Bonsoir,

Je peux t'aider mais pour cela il te faut tout d'abord respecter le règlement de ce forum en scannant uniquement le graphique sans le texte lequel doit être recopié.
Cela fait il te faudra aussi expliquer ce que tu as essayé de faire avant de demander de l'aide.

*** message déplacé ***

Posté par
diracre : Cinétique 08-02-21 à 23:35

Après pour faire plus court encore, et en fait au plus court ...

La "composante horizontale" de l'énergie cinétique reste inchangée, la "composante verticale" se transforme en énergie potentielle. A point culminant h:

mgh = \frac{1}{2}m(v_0sin\alpha)^2

Donc on obtient directement v_0 = \frac{1}{sin\alpha}\sqrt{2gh}

Posté par
chacha1995re : Cinétique 08-02-21 à 23:48

merci beaucoup, c'est très clair dans ma tête maintenant
super bonne soirée

Posté par
chacha1995re : Cinématique 08-02-21 à 23:51

Ah mince, en effet mais je n'arrive pas à supprimer mon post ...

*** message déplacé ***

Posté par
chacha1995re : Cinématique 08-02-21 à 23:55

Pour la résolution,
je me suis dis

selon x, x(t) = VocosA*t + Xo donc 1 m = VocosA*t donc t = 0,1/cosA
et selon y, Vy = VosinA - g*t
donc v(0,1/cosA) = VosinA - g (0,1/cosA)
                                            = 10 * (1,5/AP) - 1/(1/AP)
                                             =15/AP-AP

sin A = 1/AP
et AP^2= 1^2 + 1,5^2 soit AP =1,80

mais je trouve du coup v = 6,53

*** message déplacé ***

Posté par
chacha1995re : Cinématique 09-02-21 à 00:00

je viens de me rendre copte que je n'ai calculer que Vy(P) alors que V(P) = Vx + Vy

Vx(P)= Vo x t = 10 * 0,1 / cos A = AP soit 1,8

et donc V(P)= 1,8 + 6,53 = 8,33

*** message déplacé ***

Posté par
odbugt1re : Cinématique 09-02-21 à 00:29

Il ne t'est pas possible de supprimer ton post.
La solution consiste à reposter dans ce même topic l'image du graphique (sans le texte) et de recopier le texte.


*** message déplacé ***

Posté par
odbugt1re : Cinématique 09-02-21 à 09:13

L'image a été recadrée par un modérateur.
Il te suffit donc de recopier l'énoncé.

*** message déplacé ***

Posté par
chacha1995re : Cinématique 09-02-21 à 10:59

Il faut calculer la vitesse au point P sachant que Vo = 10 m/s

*** message déplacé ***

Posté par
odbugt1re : Cinématique 09-02-21 à 11:58

Je suppose que :
a) les frottements sont négligés.
b) ce que tu appelles V0 est la vitesse du mobile au point A.
c) sauf indication contraire de l'énoncé la valeur de g est g = 9,8 m/s²


Si mes suppositions sont exactes la seule force à prendre en considération est le poids.
La méthode que tu emploies est loin d'être la plus simple et de plus tu y as commis des erreurs.
Il suffit d'appliquer le théorème de l'énergie cinétique ou bien la conservation de l'énergie mécanique entre les points A et P pour répondre à la question posée.

*** message déplacé ***

Posté par
chacha1995re : Cinématique 09-02-21 à 15:14

Quand je fais mgH1 - mhH2 = 1/2 m v[/sup]- 1/2 m v[sup] je ne trouve pas cà

*** message déplacé ***

Posté par
chacha1995re : Cinématique 09-02-21 à 15:18

voici mon raisonnement

Cinématique

*** message déplacé ***

Posté par
chacha1995re : Cinématique 09-02-21 à 15:19

Ah c'est bon j'ai vu mon erreur, j'ai inversé les deux hauteurs. Merci beaucoup

*** message déplacé ***

Posté par
chacha1995re : Cinématique 09-02-21 à 15:34

En fait non... je ne comprends pas pourquoi on ne tient pas compte de l'angle ??

Car j'ai typiquement un exercice similaire où on doit tenir compte de l'angle

*** message déplacé ***

Posté par
chacha1995re : Cinétique 09-02-21 à 15:35

En fait non je ne comprend pas car j'ai un autre ego où on ne tient pas compte de l'angle ...

Posté par
chacha1995re : Cinématique 09-02-21 à 15:36

Car pour être juste il faut la composant verticale de V dans l'équation c'est Vo*SinA

*** message déplacé ***

Posté par
odbugt1re : Cinématique 09-02-21 à 16:38

Donc, bien que tu ne le dises pas je suppose que tu as décidé d'appliquer la conservation de l'énergie mécanique.
Je commence par choisir un niveau de référence des énergies potentielles de pesanteur.
On convient que ce niveau de référence pour lequel l'énergie potentielle de pesanteur est nulle correspond à un plan horizontal passant par le point A

Energie mécanique en A : EmA = (1/2) m (VA)² + 0 =  (1/2) m (VA)²

Energie mécanique en P : (1/2) m (VP)² + m g h ( avec h = yP - yA )

Conservation de l'énergie mécanique :
  (1/2) m (VA)²  = (1/2) m (VP)² + m g h
ce qui donne après simplification :

V_P =  \sqrt{ V_A^2 - 2gh}  

AN : VA = 10m/s    ;   g = 9,8 m/s²  ;    h = yP - yA = 2,5 - 1 = 1,5m

V_P =  \sqrt{ 10^2 - 2*9,8*1,5}=8,4m/s

*** message déplacé ***

Posté par
chacha1995re : Cinématique 09-02-21 à 16:47

Oui je suis tout à fait d'accord avec vous, c'est également ce que j'ai fait mais pourtant dans un autre exercice similaire pour la vitesse on me fait entrer la composante sinA.
et je ne comprend pas pourquoi dans l'un on le fait et pas dans l'autre ...

C'est cet exercice là
Une balle est lancée sous un angle de 60°par rapport à l'horizontale. Elle atteint une hauteur maximale de 2m. Que vaut la vitesse initiale ?
3,6
7,2
10,4
14,0 m/s

là réponse consiste à dire que mgh = m (VoSinA)2 / 2 car la hauteur se considère sur la composante Y. et la composante Y de la vitesse est VoSinA


Donc ma question c'est pourquoi dans mon exercice de cette page on ne prend pas en compte la composante verticale ?

*** message déplacé ***

Posté par
odbugt1re : Cinématique 09-02-21 à 17:35

Ces deux exercices, bien que ressemblants ne sont pas identiques :

Dans les deux cas il s'agit de calculer la vitesse finale du mobile, mais pas à partir des mêmes données initiales :
Dans un cas tu disposes de la vitesse initiale et de l'altitude atteinte (grâce au graphique) , dans l'autre cas tu disposes de la valeur de l'angle de départ et de la hauteur atteinte.

On adapte la stratégie de résolution en fonction des données.

*** message déplacé ***

Posté par
chacha1995re : Cinématique 09-02-21 à 17:55

Je pense avoir compris, merci beaucoup pour le temps consacré à ces explications.
C'est gentil.

Charlotte

*** message déplacé ***

Posté par
diracre : Cinétique 09-02-21 à 18:12

Tu as plusieurs égos? Aïe ... (tu me diras je n'en ai qu'un mais il est sur dimensionné )

Ne connaissant pas l'autre exo, peux tu essayer de préciser l'étape du raisonnement où tu "décroches"?

Posté par
chacha1995re : Cinétique 09-02-21 à 18:38

Ahah oups, erreur de frappe :p

En gros il faut calculer la vitesse au point P sachant que Vo = 10 m/s et que les frottements sont négligés.

Ici la résolution et d'utiliser également la relation de conservation d'énergie mécanique
Soit mgZa + 1/2m*Va^2 = mgZp + 1/2m*Vp^2
bref et dans ce cas on trouve bien la bonne réponse mais on utilise pas les sin ... ?

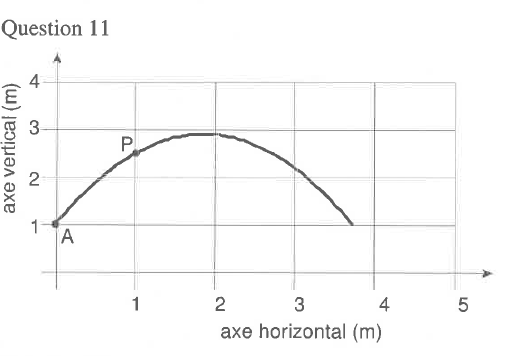
Cinétique

Posté par
gbm Webmasterre : Cinétique 09-02-21 à 19:23

Bonsoir à tous,

@ chacha1995 :

attentionextrait de c_faq la FAQ du forum :

Q03 - Pourquoi ne faut-il pas faire du ''multi-post'' ?

Posté par
gbm Webmasterre : Cinétique 09-02-21 à 19:30

Après avoir relu plus attentivement les deux sujets, je me rends compte qu'il n'étaient pas rigoureusement les mêmes, au temps pour moi

Pour éviter cela, chacha1995, pense bien à poster ton sujet en recopiant le texte et en joignant le schéma illustratif. Par bribes ça devient plus délicat à distinguer.

Puis dans un deuxième temps ces pistes, ça évitera de cette façon les confusions pour la modération.

@ dirac / odbugt1 : désolé pour l'erreur ...

Posté par
diracre : Mouvement d'un projectile dans un champs de pesanteur 10-02-21 à 07:52

Hello

En essayant de reconstituer l'histoire, dans "l'autre exercice":

Tu écris bien la conservation de l'énergie mécanique:

Em_A = Em_P = Ep_A+c_A = Ep_P+Ec_P = mgy_A + \frac{1}{2}mv_A^2 = mgy_P + \frac{1}{2}mv_P^2

Or V_A^2 = V^2_{x,A} + Vy^2_A

Posté par
diracre : Mouvement d'un projectile dans un champs de pesanteur 10-02-21 à 08:01

Zut, j'ai appuyé sur le mauvais bouton... je poursuis

V_A^2 = V^2_{x,A} + V^2_{y,A}  et   V_P^2 = V^2_{x,P} + V^2_{y,P}

Donc  mgy_A + \frac{1}{2}mv_A^2 = mgy_P + \frac{1}{2}mv_P^2

Devient  mg(y_P-y_A) = \frac{1}{2}m(V^2_{x,A} + V^2_{y,A}  -   V^2_{x,P}  - V^2_{y,P})

Avec  V^2_{x,A} = V^2_{x,P}

Donc  mg(y_P-y_A) = \frac{1}{2}m(V^2_{y,A}  -   V^2_{y,P})

Lorsque P est le sommet:  y_P-y_A = h  et V_{y,P} = 0

Donc  mgh = \frac{1}{2}mV^2_{y,A} = \frac{1}{2}mV^2_{A} = \frac{1}{2}mV^2_{A}sin^2\alpha

On a bon?






Posté par
chacha1995re : Mouvement d'un projectile dans un champs de pesanteur 11-02-21 à 12:58

Non justement la réponse ne tient pas compte des sinus ..

Energie mécanique en A : EmA = (1/2) m (VA)² + 0 =  (1/2) m (VA)²

Energie mécanique en P : (1/2) m (VP)² + m g h ( avec h = yP - yA )

Conservation de l'énergie mécanique :
  (1/2) m (VA)²  = (1/2) m (VP)² + m g h
ce qui donne après simplification :

V_P =  \sqrt{ V_A^2 - 2gh}  

AN : VA = 10m/s    ;   g = 9,8 m/s²  ;    h = yP - yA = 2,5 - 1 = 1,5m

V_P =  \sqrt{ 10^2 - 2*9,8*1,5}=8,4m/s

Posté par
diracre : Mouvement d'un projectile dans un champs de pesanteur 11-02-21 à 17:45

"Non justement la réponse ne tient pas compte des sinus .. "

Bien sûr, les question ne sont pas les mêmes ... donc aucune raison que les réponses le soient

Dans l'exercice "dirac":  on te demande la vitesse initiale connaissance la hauteur maximale atteinte: la connaissance du sinus est impérative car c'est la composante verticale de la vitesse initiale qui détermine cette hauteur

Dans l'exercice "odbugt1" (que je salue bien): tu n'as effectivement pas besoin de connaitre l'angle de tir car tu connais la vitesse initiale, sa norme en fait, et que tu disposes donc de toutes les informations nécessaires en utilisant la conservation de l'énergie mécanique !

Posté par
odbugt1re : Mouvement d'un projectile dans un champs de pesanteur 11-02-21 à 17:47

Pour une vitesse initiale donnée (ici 10m/s) la vitesse atteinte au point P (8,4 m/s) ne dépend que de la différence d'altitude entre les points A et P et ne dépend pas de l'angle de lancement.

Autrement dit : Quel que soit l'angle de lancement  (permettant d'atteindre le point P) la vitesse en ce point P dont l'altitude par rapport à A est de 1,5m aura pour valeur 8,4m/s
Les différents points P correspondant aux différents angles de lancement ont tous la même ordonnée mais pas la même abscisse.

Posté par
odbugt1re : Mouvement d'un projectile dans un champs de pesanteur 11-02-21 à 17:49

Post "croisés" avec Dirac que je salue à mon tour

Posté par
chacha1995re : Mouvement d'un projectile dans un champs de pesanteur 11-02-21 à 17:56

Bon je pense avoir compris ahah !! j'espère

Merci beaucoup à vous deux pour les explications, c'est vraiment top !!! Vous m'avez beaucoup aidé !!


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !