Ce que je pense avoir compris :

Le mouvement de disque est un roulement c'est-à-dire une translation du centre du disque avec rotation autour de ce centre.

On distingue deux phases :
a) Entre O et E un roulement sans glissement pour lequel la vitesse "v" du centre de (D) est lié à sa vitesse angulaire "ω" par la relation v=Rω
b) Entre E et F une "chute", phase dans laquelle le centre de (D) possède un mouvement parabolique classique accompagné d'une rotation à vitesse constante de rotation autour de ce centre.

L'énergie cinétique de (D) est la somme de son énergie cinétique de translation et de son énergie cinétique de rotation.

Ce qui n'est pas normal :
Le disque est lancé en O avec une vitesse v₀ de 5m/s et tu trouves que cette vitesse est devenue 5,8m/s en E donc tu trouves que v_E > v₀

Bon, je refais le TEC avec à la fois V et pour trouver V_E
Puis, pour _E je divise par R V_E
Est-ce la bonne démarche ?

Oui !

1) Syst{centre de gravité de (D)} en translation
TEC(O vers E)
E_cE-E_cO=-Mglsin
Donc V_E= 3,4 m/s
2) une question, la vitesse du centre de gravité est-elle égale aux vitesse linéaires de tous points sur le disque ?
En fait, on n'a pas encore vu de type comme celui-ci.

Question 1 :
Je ne trouve pas le même résultat que toi et comme tu ne détailles pas ton calcul je ne peux pas savoir d'où provient la différence.

2) Non.
Il est clair, qu'un point situé (par exemple) à la périphérie du disque n'a pas la même vitesse que celle de son centre de gravité.

1) TEC:
(1/2) M V_E²-(1/2) M V₀²= -Mgl sin
J'ai considéré que G( je crois qu'on va le noter ainsi le centre de gravité pour ne plus écrire long) comme un corps ponctuel classique en translation.

Comme déjà indiqué précédemment ( 06-09-19 à 10:21)

L'énergie cinétique de (D) est la somme de son énergie cinétique de translation et de son énergie cinétique de rotation

Tu n'as tenu compte que de la translation de (D) et pas de sa rotation.

TEC(OE)
(1/2) J^._E²+ (1/2) M V_E² -(1/2) J^.₀² -(1/2) MV₀²= W(P)=-Mg l sin

Avec, ^._E= V_E/R
Et ^.
₀= V₀/R

D'où, V_E=(-4/3 gl sin + V⁰²)
AN: V_E= 4 m.s^-1

Et ^._E= V_E/R= 20 rad.s^-1

C'est exact, car la seule force qui travaille est le poids de (D)

3) a) il demande la hauteur maximale atteinte par G
Pour ce faire il faut trouver l'équation horaire et l'équation cartésienne de la trajectoire de G
On assimile le disque à G qui est lancé avec V_E et on fait comme d'habitude pour les équations horaires et cartésienne
Est-ce correct ma démarche ?

Oui, on peut répondre à cette question en utilisant la méthode que tu décris.
L'équation cartésienne n'est pas indispensable, même si on peut, en effet, l'utiliser.

On peut aussi utiliser le théorème de l'énergie cinétique ou la conservation de l'énergie mécanique.

Ah bon, et comment ?
Je voudrais bien connaître cette méthode.

On peut appliquer le théorème de l'énergie cinétique entre les points M et S (voir figure).

Merci,
Une question sur la vitesse linéaire et angulaire
On a vu que la vitesse v₀ et v_E s'appliquent en G
Et pour l'énergie cinétique du système, on additionne l'énergie cinétique de translation et de rotation
Et pour^. on a fait v₀/R mais la formule ^.=v/R n'est elle valable que pour une vitesse l'inéaire s'appliquant à un  pt se situant en une distance R du centre ?
Et de plus, V n'est-t-elle pas variable en fonction de la distance R du centre et du pt ?

Tout les points ont la même vitesse angulaire
Leurs vitesses linéaires dépendent de leurs distances r au centre selon la relation v=r*
Pour un point situé à la périphérie r=R
Si le disque roule sans glisser la vitesse linéaire du centre de gravité est liée à la vitesse angulaire par la relation v = R ( voir mon post du 06-09-19 à 10:21 )

Pour la nature du mvt du disque durant le saut
SYS{G} en translation
D'après le TCI (car la masse du cylindre est concentrée en G n'est ce pas ?)
Et on voit que a est constante
Est-ce qu'il faut aussi passer au TAA pour le système cylindre en rotation ?

Oui, le centre de gravité de (D) va donc avoir un mouvement parabolique classique.
On admet que sa vitesse initiale de translation a même direction et même norme que la vitesse finale de la phase précédente.

Pendant la chute, la somme des moments des forces extérieures qui s'exercent sur le disque est nulle. Il en résulte que la vitesse de rotation du disque est constante et égale à sa vitesse de rotation finale en fin de phase précédente (20 rad/s)

Heureusement..
Pour c) je crois que ça ira
d) comment trouver ce nbe de tours durant le saut?

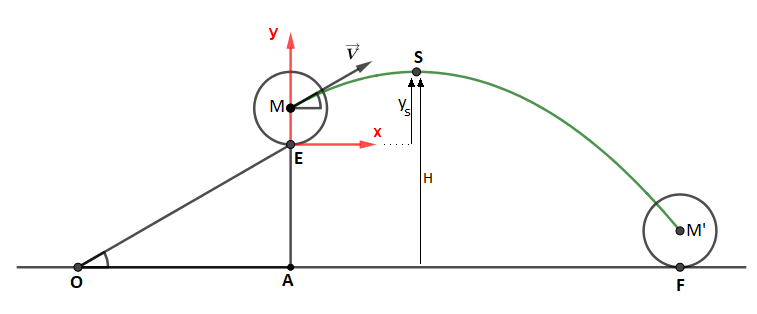
La vitesse de rotation étant connue, il te faut calculer le "temps de vol" entre M et M' (Voir mon schéma)
Le nombre de tours s'obtient alors très simplement.

Ok, merci infiniment

Vérification :
V_F=5m/s
Est-ce que la durée du saut est 0,4s
Et le nbe de tours est 1,27 tours?

Désolé. Je ne vérifie pas de résultats numériques non justifiés.

Oups
Bon pour V_F, TEC(E vers F)
Je prends les énergies cinétiques de la translation et de la rotation et il n'y que le poids qui travaille en l'air
Au final, V_F=5m.s-1

Après, pour la durée du saut
Dans(E,x,y)

Sur (E,y)
0=-(g/2)t²+V_Et
t≠0, donc (-g/2)t+V_E=0
Donc t=0,4s

Et =^.t+_E
Et 1tour=2π
Donc nbe de tours=1,27

Je prends les énergies cinétiques de la translation et de la rotation et il n'y que le poids qui travaille en l'air
Au final, VF=5m.s-1

La méthode est bonne.
Je ne trouve pas le même résultat numérique.

Sur (E,y)
0=-(g/2)t²+VEt
Non
-(g/2)t²+V_E t  = -L sin()

C'est vrai,
Il faut bien regarder...

Et la démarche pour ^., elle est bonne ?

Je ne sais pas.
Comme tu ne définis pas tes notations je préfère ne pas me prononcer.

Comme il s'agit d'un mouvement de rotation uniforme,
=^.t+_E
Avec_E=0

Donc, =^.t
Est ce correct ?

Tu ne définis toujours pas tes notations !

Si ton =^.t
équivaut à  
relation dans laquelle est l'angle cherché (en rad) ,    la vitesse angulaire (en rad/s) et  "t"  la durée du vol alors oui la relation que tu proposes est correcte.

Oui... c'est la vitesse angulaire que je voulais écrire
Je ne sais pas comment l'écrire en LaTex

En LaTex    s'écrit  \dot{\theta}

Bon, merci pour l'exercice et merci pour le tuyau