Inscription / Connexion Nouveau Sujet
Mouvement compliqué
Svp aider moi ici cet exercice m'embête .
Énoncé :une voiture A est arrêté sur une route rectiligne horizontale horizontale à une distance d1=3m d'un feu rouge. Lorsque le feu passe au vert à l'instant t=0 la voiture démarre avec une accélération constante a=3m/s².
Au même moment un motard roulait à une vitesse constante V2=54km/h se trouve à une distance d2=24m de la voiture
La voiture et le motard considérés comme des point matériels sont repérés à l'instant t à l'aide de leur vecteur position respectifs OA(vecteur)=x1i et OM(vecteur)=x2i. On choisi comme origine des espaces la position du feu tricolore.
1/Déterminer les lois horaires x1(t) et x2(t) de la voiture et du motard respectivement
2/Déterminer les instants de dépassement ainsi que les positions de la voiture et du motard à ces instants
3/si le motard roulait à la vitesse V2=36km/h pourrait-il rattraper la voiture?
4/calculer dans ce cas l'instant pour lequel la distance qui sépare le motard de la voiture est minimale.
5/En déduire cette distance.
6/ quelle est la vitesse minimale
du motard à partir de laquelle il pourra rattraper la voiture ?
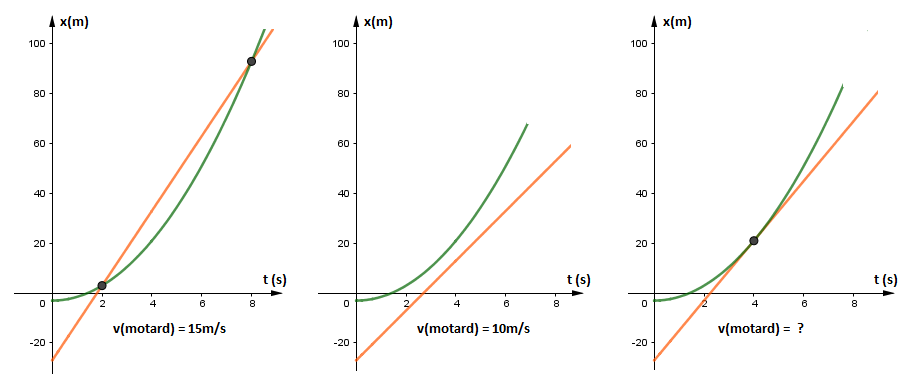
Je vous donne le schéma
1/ les lois horaires
**celle de la voiture
a=cste --->MRUA
X1(t)=3/2t²-3
**celle du motard
V=cste ,--->MRU
X2(t)=15t-27
2/les instants des dépassements
X1(t)=X2(t) la résolution de cette équation donne t1=2s et t2=8s
Les instants des dépassements
On trouve x1=x2=3m
Et x1=x2=93m
3/la loi du motard dans ce cas x2(t)=10t-27
X1=x2 cette équation du 2nd degré admet un discriminant négatif donc pas de rattrapage dans ce cas
Voici deux manières de traiter cette question :
Soit exprimer en fonction du temps la distance D qui sépare les deux véhicules, puis rechercher grâce aux outils mathématiques la date θ qui rend D minimale.
Soit remarquer que la distance D diminue tant que la vitesse de la moto est supérieure à celle de la voiture, puis augmente quand l'ordre de ces vitesses est inversé.
On en conclut alors que D est minimale à la date θ pour laquelle les vitesses des deux véhicules sont égales.
Une bonne idée est d'essayer les deux méthodes et de constater qu'elles conduisent au même résultat.
J'ai essayé ceci
Soit dmin la distance minimale
dmin=x2-x1=3/2t²-3-(10t-dmin-3) le calcul donne t=6,66s est-ce que c'est correct ?
Pardon inutile ce que je viens de poster il y avait un retard de votre message c'est la raison pour laquelle j'ai essayé cela mais merci beaucoup quand même
En utilisant la méthode
On a : V(voiture)=3t et Vm=10
L'égalité donne t=3,33s?????
Pour la méthode 1 j'ai pas bien saisi mais j'ai essayé ceci d=10t. Mais je n'arrive pas à pouvoir continuer
Méthode 1 :
x1 = 1,5t²
x2 = 10t-3
D = x1 - x2 = 1,5t² - 10t + 3
D est minimale quans sa dérivée par rapport au temps s'annule :
D'(t) = 3t - 10
D'(t) = 0 pour θ = 10/3 = 3,33s
C'est parce que j'ai bêtement confondu les données !
En réalité :
x1 = 1,5t² - 3
x2 = 10t - 27
D = x1 - x2
D = 1,5t² - 10t + 24
D'(t) = 3t - 10
D'(t) = 0 pour θ = 10/3 = 3,33s
A cette date D = 7,33m
Question5
La vitesse minimale du motard pour qu'il ait rattrapage
X1=1,5t²-3
X2=vt-10,33
L'égalité entre x1 et x2 donne v =7,9m/s soit 26km/h. Ce résultat vous semble-t-il correcte?
Non
Je ne comprends pas d'où provient 10,33
Pense à vérifier la vraisemblance de ton résultat :
Tu as montré (question 3 ) qu'avec une vitesse de 10 m/s le motard ne rattraperait pas la voiture.
Aucune chance qu'il y parvienne avec une vitesse de 7,9 m/s !
Le résultat attendu est forcément compris entre 10m/s ( pas de rattrapage ) et 15m/s