Inscription / Connexion Nouveau Sujet
modélisation du comportement de la lumière
Bonsoir
A l'aide d'un banc optique horizontal et orienté dans le sens de propagation de la lumière mesurer les distances algébriques lentille - Objet OA et lentille-image OA'
en établissant un tableau de correspondance pour une dizaine de valeurs de OA
les distances seront exprimées en mètres dans le tableau de mesure
j'ai relevé des mesures pour lentille objet et comme on est placé dans le sens de propagation de la lumière , c'est à dire de la gauche vers la droite les valeurs de la première colonne sont donc précédées du signe -
| OA (en m) | OA' (en m) | |||||
| -0,50 | -5,0 * 10^-1 | 1,17 | ||||
| -0,65 | -65 * 10-2 | 0,709 | 70,9 * 10 - 2 | |||
| -0,80 | -80 * 10 -2 | 0,586 | 58,6 * 10^-2 | |||
| -0,90 | -90 * 10^-2 | 0,546 | 54,6 * 10-2 | |||
| -0,105 | -10,5 *10-2 | 0,508 | 50,8 * 10-2 | |||
| -0,110 | -110 * 10-2 | 0,495 | 49,5 * 10-2 |
2) montrer que la fonction f telle que
où k est une constante qui sera déterminée graphiquement
3) estimer la précision des mesures de OA' et de OA et en déduire celle sur k
Bonjour.
Concernant le tableau de valeurs, je note une étourderie...
Dernière ligne, colonnes 1, 2 et 5 : et non
et
et non
Par ailleurs, je ne vois pas l'intérêt d'écrire le contenu des deux dernières colonnes avec des puissances de 10, on aurait plus simplement
Pour la suite, faites la représentation graphique demandée, identifiez la courbe obtenue et déterminez son équation.
En cas de difficultés, jetez un coup d'oeil au post dont voici le lien, où un travail similaire était demandé 
![]() Modélisations d'une lentille mince 1ère S.
Modélisations d'une lentille mince 1ère S.
A plus.
pour la dernière ligne de la colonne 1 en fait je me suis trompé
les données sont respectivement 1,05 mètre et 1,10 mètre et non pas
je recommence le tableau
| OA (en m) | OA'(en m) | |||||
| -0,50 | 1,17 | |||||
| -0,65 | 0,709 | |||||
| -0,80 | 0,586 | |||||
| -0,90 | 0,546 | |||||
| -1,05 | 0,508 | |||||
| -1,10 | 0,495 |
pour le calcul de
je divise
le suivant
je divise
je suis un peu perdu dans les calculs
quand j'obtiens 0,0154 avec la calculatrice
quelle est l'unité de mesure de 0,0154 ??
j'ai oublié de vous dire Bonjour
et aussi de vous remercier de m'avoir répondu
j'ai voulu aller trop vite en refaisant le tableau
pour le calcul de
je divise
Indiquez moi le modèle de votre calculatrice, je vais vous donner la procédure à suivre.
le suivant
je divise
je suis un peu perdu dans les calculs
quand j'obtiens 0,0154 avec la calculatrice
quelle est l'unité de mesure de 0,0154 ??
Bonsoir ,
avec les données suivantes
| 1/OA (en m-1 | - 2,00 | -1,54 | -1,25 | -1,11 | -0,95 | -0,91 |
| 1/OA' (en m -1- | 0,86 | 1,4 | 1,7 | 1,8 | 2,0 | 2,0 |
j'obtiens une droite qui coupe l'axe des ordonnées en traçant une représentation graphique avec
pour échelle j'ai pris 1 carreau pour 0,5 cm
en abscisse j'ai placé les valeurs négatives (celles de 1/OA )
et en ordonnée les valeurs 086 ; 1,4 ; 1,7 ; 1,8 ; 2,0 en prenant aussi 1 carreau = 0,5 cm
la droite coupe l'axe des ordonnée au point y = 3
pour calculer le coefficient directeur de la droite
j'ai pris le point de coordonnées
j'obtiens a =
j'essaie avec un autre couple de points
j'obtiens a = 1,25
donc on peut dire que le coefficient directeur est à peu près 1
la représentation graphique de
j'ai cette question
quand on demande de montrer que la fonction f telle que
il s'agit de la fonction qui a
c'est cela ?
Bonsoir
on demande aussi d'estimer la précision des mesures de OA et OA'
et en déduire celle de k
pour la précision de mesures dans la première colonne
-----> celles-ci sont négatives parcequ'on est dans le sens de propagation de la lumière
donc OA , c'est en fait AO
c'est cela ??
Ce que vous avez fait est plutôt bien.
Une seule chose me chagrine un peu, c'est la détermination du coefficient directeur de la droite obtenue.
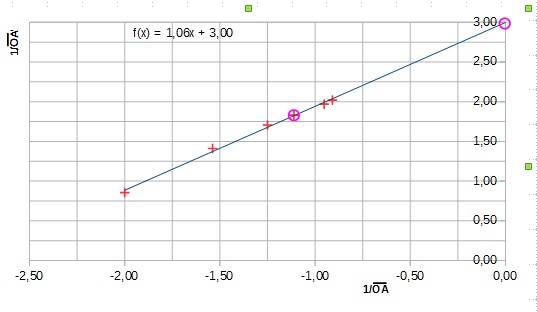
En reprenant vos résultats de mesures, j'ai tracé la représentation graphique demandée à l'aide d'un tableur (cf image jointe).
L'équation donnée par l'ordinateur pour la droite obtenue est :
Le coefficient directeur obtenu (1.06) est donc assez éloigné de ce que vous proposez (1.17 puis 1.25)..
Ce qui est en cause, c'est évidemment le choix du couple de points retenus pour le calcul de ce coefficient directeur.
Si vous voulez vous rapprocher de la valeur théorique attendue (càd 1), il faut choisir des points bien situés sur la droite, même s'ils ne correspondent pas à des mesures effectivement réalisées.
En retenant les deux points cerclés en rose sur la courbe (0 ; 3) et (-1.11 ; 1.83), on obtient pour ce coefficient directeur, la valeur suivante :
Cela paraît plus correct non ?
L'ordonnée à l'origine est, quant à elle lue directement sur le graphe k = 3.0 m-1. C'est bien ce que vous avez trouvé.
Pour la suite...
on demande aussi d'estimer la précision des mesures de OA et OA'
et en déduire celle de k
Si vous pensez que OA est mesuré à 2 mm près, on peut écrire par exemple que pour OA = 0.90 m on a, en fait (0.90 - 0.002)
 OA
OA  (0.90 + 0.002) càd encore 0.898
(0.90 + 0.002) càd encore 0.898  OA
OA  0.902 tout ceci étant en m évidemment.
0.902 tout ceci étant en m évidemment.
On aura alors , pour 1 / OA, les limites suivantes (en m-1) :
1 /0.902
 1 / OA
1 / OA  1 / 0898 càd encore 1.108
1 / 0898 càd encore 1.108  1 / OA
1 / OA  1.113
1.113
Je vous ai donné des pistes, à vous de les exploiter pour conclure ce compte rendu.
Il me semble que vous êtes bien parti !
A plus.
Bonsoir
je viens d'avoir une interdiction de communiquer pour utilisation de plusieurs comptes
de quel autre compte s'agit il ??
je n'y comprends rien ?
puis je parler avec le modérateur
merci
Bonjour monsieur ,
L'accés au Forum m'était interdit lorsque j'ai voulu reprendre contact avec vous , en effet il y avait une image avec un gendarme muni d'une matraque !!!
me reprochant un accès sur le forum avec plusieurs comptes
à vrai dire je n'y comprends rien !
Je n'ai aucunes mauvaises intentions (bien au contraire ..........)
et je n'utilise que ce compte (quel est l'autre compte qui visiblement pose problème ???)
----> je voulais répondre à votre message , pour vous remercier :
- pour le temps que vous avez passé pour refaire la représentation graphique avec les mesures
- pour vos encouragements également
mais revenons à la Physique !!
j'ai le sentiment que je ne comprends pas bien ce qu'est une mesure en Physique
(et cela doit remonter au collège , il y a peut être des TP qui n'ont pas été réalisé)
- si je mesure la distance lentille -objet sur un banc optique (orienté dans le sens de propagation de la lumière)
je vais noter la mesure lue , par exemple OA = 90 cm
- si je dois pipeter un volume de 10 ml , je vais noter 10 ml sur la feuille de TP
maintenant si mon professeur me pose cette question : ' à combien près avez vous pu déterminer la valeur mesurée ?
et bien le résultat va être le suivant -----> je vais faire rire toute la classe
je suis incapable de répondre à cette question
il y a autre chose que je ne comprends pas , quand vous me dites :
on peut écrire que pour OA = 0,90 m , on a (0,90 -0,002) < OA < (0,90 + 0,002)
comme nous sommes dans le sens de propagation de la lumière ,c'est à dire de la gauche vers la droite , il me semble que la valeur de OA doit être négative
je ne comprends pas pour quelle raison vous avez pris OA = 0,90 m
il y a autre chose que je ne comprends pas , quand vous me dites :
on peut écrire que pour OA = 0,90 m , on a (0,90 -0,002) < OA < (0,90 + 0,002)
comme nous sommes dans le sens de propagation de la lumière ,c'est à dire de la gauche vers la droite , il me semble que la valeur de OA doit être négative
Vous avez tout à fait raison concernant le signe de
- si je mesure la distance lentille -objet sur un banc optique (orienté dans le sens de propagation de la lumière)
je vais noter la mesure lue , par exemple OA = 90 cm...
...maintenant si mon professeur me pose cette question : ' à combien près avez vous pu déterminer la valeur mesurée ?
Je vous fait part de mon expérience personnelle, si la précision sur OA est bonne (de l'ordre de quelques mm), en revanche la précision sur OA' l'est moins ; l'opérateur va juger subjectivement de la position de l'écran qui donne l'image la plus nette, mais si on déplace l'écran de 1 cm à droite ou à gauche de cette position, cela a peu de conséquences sur la netteté de l'image. De pus, l'imprécision augmente si la salle de TP n'est pas correctement obscurcie...
- si je dois pipeter un volume de 10 ml , je vais noter 10 ml sur la feuille de TP
maintenant si mon professeur me pose cette question : ' à combien près avez vous pu déterminer la valeur mesurée ?
-des facteurs liés à la qualité du matériel utilisé : il existe différentes gammes de matériel, en gros plus c'est cher, plus c'est précis.
-des facteurs liés à l'adresse des opérateurs : il y a des personnes soigneuses et appliquées mais aussi de vrais sagouins !
Avec le matériel des lycées et des opérateurs raisonnablement avertis, la précision sur le volume mesuré lors d'un pipetage doit être de l'ordre de 1 à 2 %.
L'accés au Forum m'était interdit lorsque j'ai voulu reprendre contact avec vous , en effet il y avait une image avec un gendarme muni d'une matraque !!!
me reprochant un accès sur le forum avec plusieurs comptes
à vrai dire je n'y comprends rien !
A une prochaine fois.

A, oui, j'ai oublié cette dernière question...
je ne comprends pas pour quelle raison vous avez pris OA = 0,90 m
Bonsoir monsieur ,
merci de m'avoir répondu
en fait c'est ce calcul que je ne comprends pas
(0.90 - 0.002) < OA <(0.90 + 0.002)
Si on mesure, pour OA 90 cm, avec une incertitude sur la mesure de 2 mm (2 mm = 0,2 cm), cela signifie que la valeur réelle de OA est quelque part entre 90 - 0,2 = 89,8 cm et 90 + 0,2 = 90,2 cm.
OK ?


