Bonjour à tous !

Je rencontre quelques soucis sur un exercice dont l'énoncé est le suivant :

Il est possible de mesurer la vitesse d'écoulement d'un fluide (liquide ou gaz) dans une canalisation en utilisant des ondes ultrasonores.
La vitesse de propagation de l'onde ultrasonore V dans un fluide en mouvement s'exprime en fonction de la vitesse de fluide Vf et de la vitesse de l'onde Vo dans ce même fluide lorsqu'il est à l'équilibre par : V=Vf+Vo
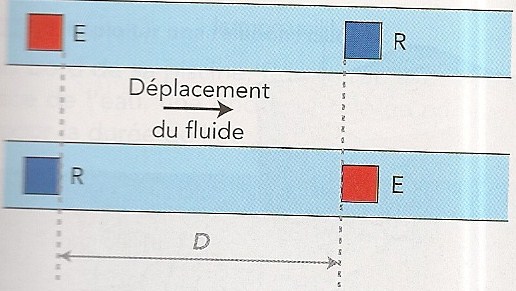
Un émetteur ultrasonore émet des ondes qui sont reçues au bout d'une durée t par un récepteur situé a une distance D de l'émetteur. L'émetteur E est soit en amont soit en aval du récepteur.

Lorsque l'émetteur est en amont, la durée de propagation est ∆t1, s'il est en aval, cette durée est ∆t2.

1) Exprimer la valeur de la vitesse V de l'onde ultrasonore en fonction de Vo et de Vf dans les deux cas
2) Exprimer ∆t1 et ∆t2 en fonction de Vo, Vf et D. Quelle est la plus petite durée ?
3) Montrer que l'écart entre ces durées ∆t=∆t2-∆t1 est : ∆t=(2*D*Vf)/(Vo²-Vf²)
4) Au cours d'une expérience dans l'eau, pour D=1.98m, on mesure ∆t=2.32µs. Quelle est la valeur de Vf si Vo=1480m.s^-1 ?
5) Quelles peuvent être les sources d'incertitudes dans cette méthode de mesure de la vitesse du fluide ?

J'ai déjà cherché et trouvé l'exercice sur le site mais il s'avère que je ne comprends pas très bien comment on arrive au résultat de la question 4 !

Mes réponses :

1) V1 = Vo+Vf (cas a) --> le fluide se déplace vers le récepteur
     V2=Vo-Vf (cas b) -->  le fluide se déplace vers l'émetteur

2) On sait que ∆t = d / V , donc :

∆t1 = D / (Vo+Vf)  ;  ∆t2 = D / (Vo-Vf)

La plus petite durée sera ∆t1 (car, dans ce cas, on divise D par une plus grande vitesse que pour ∆t2)

3) On veut montrer que ∆t = [ 2*D*Vf ] / [ Vo²-Vf² ] = ∆t2 - ∆t1

On sait que,  ∆t1= D / (Vo+Vf)
             et que ∆t2 = D / (Vo-Vf)

donc ∆t2 - ∆t1 = [ D / Vo-Vf ] - [ D / Vo+Vf ]
                           <=> [ D(Vo+Vf) - D(Vo-Vf) ] /  [ (Vo-Vf)(Vo+Vf) ]
                           <=> [ D*Vo + D*Vf - D*Vo + D*Vf ] / [ Vo² + Vo*Vf - Vf*Vo - Vf² ]
                           <=> [ 2*D*Vf ] / [ Vo²-Vf² ]

4) Je suis bloquée ici, mais je suppose qu'il faut mettre la formule de ∆t sous la forme ax²+bx+c=0, remplacer les valeurs par celles connues en convertissant 2,32µs par 2,32.10 ^-6 s , puis trouver ∆, les racines etc.

5) Les incertitudes proviennent des mesures des distances et de l'exactitude des durées ∆t1 et ∆t2.

En vous remerciant d'avance