Inscription / Connexion Nouveau Sujet
Mesure d'une distance focale
Bonjour,
J'ai un exercice dont l'énoncé est le suivant:
"Au cours d'une séance de travaux pratiques, les élèves d'une classe de 1e S étudient la formation des images données
par une lentille mince convergente. Ils tracent pour cela le graphe donnant : y = 1 / OA' en fonction de : x = 1 / OA.
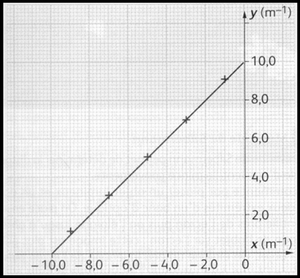
1. Quelle est la nature du graphe obtenu ?
2. En utilisant la relation de conjugaison, donner l'expression de la fonction : y = f (x). Est-elle compatible avec le
graphe obtenu ? Justifier.
3. En déduire graphiquement la vergence de la lentille étudiée. Quelle est sa distance focale ?
4. Déterminer graphiquement la position de l'image quand l'objet est placé 20 cm devant la lentille. Justifier la détermination." (voir graphique)
Cette exercice m'échappe complètement
J'ai peut être une idée pour le 2): on sait que 1/OA'=1/OF'+1/OA donc on aurait f(x)=1/OF'+x=y mais je ne suis pas du tout sûr de moi. Pouvez-vous m'aider s'il vous plaît? Merci
Bonjour,
Ce topic devrait t'aider : 
![]() DM de physique chimie sur l'optique
DM de physique chimie sur l'optique
Si tu as encore des questions, poste-les ici.

Bonsoir,
Donc si j'ai bien compris...
1)Le graphe est une droite
2)On sait que 1/OA'=1/OF'+1/OA donc f(x)=y=1/OF'+x. Elle est compatible avec le graphe car c'est une fonction affine de la forme ax+b or le graphe est une droite.
Est-ce que c'est bien ça?
Par contre je ne sais pas comment faire pour la suite...
Merci
Oui, c'est bien cela.
Tu peux ajouter que le coefficient directeur de cette droite vaut 1, ce qui est également compatible avec la relation de conjugaison.
D'après la fonction, quel est le terme qui représente l'ordonnée à l'origine ?
Et physiquement, que représente ce terme ?
Les réponses à ces deux questions te permettent de répondre à la question 3

L'ordonné à l'origine est 10m-1
On a x=1/OA OA=1/x
OA=1/x
On a y=1/OA' OA'=1/y
OA'=1/y
Physiquement, ça veut dire que si OA=-0,1m OA'=0m
C'est ça?
Merci
Je ne crois pas.
L'ordonnée à l'origine vaut bien 10 m-1
Dans l'équation y = a.x + b
l'ordonnée à l'origine vaut b
Ici
et
La relation de conjugaison est
donc
le coefficient directeur est a = 1
l'ordonnée à l'origine est
Physiquement est l'inverse de la distance focale, donc la vergence de la lentille.
C'est pour cela que tu peux avec cette identification répondre à la question 3
Vergence : 10 m-1 = 10  (= 10 dioptries)
(= 10 dioptries)
et donc
distance focale = 1/10 = 0,10 m = 10 cm
____________
Ce que l'on peut lire sur le graphique c'est que pour c'est-à-dire pour
alors
c'est-à-dire
On retrouve la propriété bien connue : quand l'objet est à l'infini, l'image est située à une distance du centre optique de la lentille égale à la distance focale.

D'accord! Merci beaucoup! Donc je récapitule pour la 4), on a OA=-20cm, donc à l'infini optique et donc dans ce cas OA' OF' donc OA'
OF' donc OA' 10cm. C'est bien ça?
10cm. C'est bien ça?
Merci beaucoup!
1/OA=1/OA'-1/OF'=-0,05
Donc on cherche OA'
Donc on a 1/OA'=1/OF'+1/OA
1/OA'=1/10+1/-20=9,95
OA'=1/9,95=0,1cm
C'est ça?

C'est faux.
Que vaut ?
Et tu peux lire le résultat sur le graphique avant de faire le calcul pour confirmation.
À noter que ce résultat doit être connu par cœur
Quand l'objet est à une distance de la lentille convergente égale à deux fois la distance focale, alors l'image ... (la suite tout à l'heure, après tes réponses)

1/OA=1/(-0,20)=-5m-1?
peut être que quand l'objet est à une distance de la lentille convergente égale à deux fois la distance focale, alors l'image est à une distance de la lentille égale à la distance objet-lentille?
Dans ce cas 1/OA'=5m-1
Et donc OA'=20cm
C'est bon?
Un bon conseil pour t'éviter bien des ennuis en optique : n'utilise qu'une seule unité de longueur : le mètre (ce n'est pas obligatoire mais c'est une bonne précaution pour les débutants ! )
_________
Oui, si alors
Ce qui se lit directement sur le graphique -5 m-1 et + 5m-1
Rappel, la distance focale vaut
Donc :
Quand l'objet est à une distance de la lentille convergente égale à deux fois la distance focale, alors l'image est de l'autre côté de la lentille, également à une distance de deux fois la distance focale, elle est renversée et de même taille que l'objet ; donc le grandissement est égal à -1
À savoir par cœur, crois-moi.



