Bonjour à tous,

J'ai à faire un exercice dont voici l'énoncé :

"Un positon de charge et de masse prénètre dans un champ électrostatique uniforme avec une vitesse initiale .
On étudie son mouvement dans un référentiel terrestre. À chaque instant, les coordonnées du vecteur accélération dans les conditions de l'expérience sont :
"

Le but de l'exercice est de déterminer les coordonnées du vecteur à chaque instant, à l'aide des coordonnées de .

Cela ne pose pas de problème si je connais les coordonnées de , mais un doute affreux m'envahit à ce sujet.

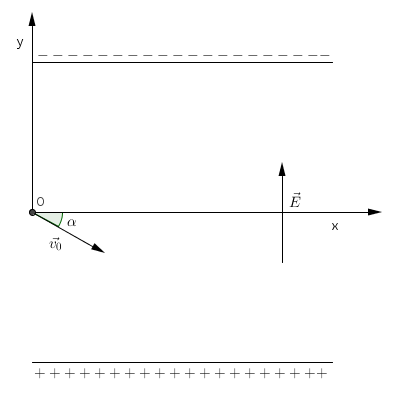
Comme vous le voyez, est dirigé vers le bas. J'ai donc noté comme coordonnées de v_0 : .
Le "moins" quant à la seconde coordonnée est selon moi due à la direction vers le bas de ce vecteur ...

Mais condidère-t-on que l'angle est orienté ? Auquel cas l'on n'aurait pas besoin d'appliquer le "moins" puisque l'angle serait lui même déjà négatif. Ce qui donnerait : .

Je ne parviens pas à trancher. Est-ce une question de convention ?

Je vous remercie.