Inscription / Connexion Nouveau Sujet
Mécanique Newtonienne
Bonsoir,
Je rencontre un problème avec un exercice traitant la notion de la mécanique Newtonienne.
Le voici:
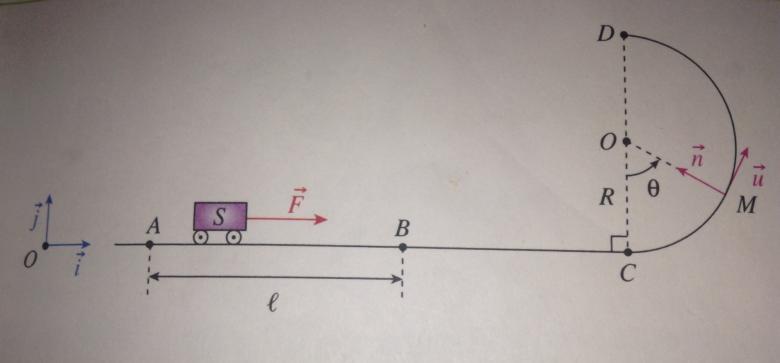
On étudie le mouvement d'un wagonnet S dans le référentiel terrestre supposé galiléen. Ce solide, de masse m, est initialement au repos en A. On le lance sur la piste ACD représentée sur la figure, en faisant agir sur lui, le long de la partie AB de sa trajectoire, une force horizontale et de valeur constante. On pose AB = l.
La portion AC de la trajectoire est horizontale et la portion CD est un demi-cercle de centre O et de rayon C; ces deux portions sont dans le même plan vertical.
La piste est parfaitement lisse et les frottements sont négligeables.
*A: Etude du mouvement entre A et B:
1)Déterminer l'accélération du wagonnet.
Voici ce que j'ai trouvé:
Grace à la deuxième loi de Newton:
2)a) Déterminer l'expression de la vitesse en fonction de F, m et x, distance parcourue.
Voici ce que j'ai essayé de faire:
et
J'isole le t dans x(t):
Et je remplace ensuite le t dans l'équation horaire v(t) pour obtenir v:
La correction m'indique cela:
et
Donc, , soit
Je ne comprends pas comment ils en sont arrivés à avoir la relation v(t) = x(t). N'est-ce pas des valeurs différentes?
Merci d'avance!
Je me suis trompé:
"La portion AC de la trajectoire est horizontale et la portion CD est un demi-cercle de centre O et de rayon C"
C'était:
La portion AC de la trajectoire est horizontale et la portion CD est un demi-cercle de centre O et de rayon R
Bonsoir,
Tu as raison : On ne peut pas écrire que v(t) = x(t) pour les raisons que tu invoques.
Ce n'est pas la seule incohérence :
Quand tu écris que :
tu égales un vecteur avec un scalaire !
Quand le corrigé écrit que :
Non seulement il affirme qu'une vitesse est égale à une longueur, mais lui aussi il égale un vecteur avec un scalaire.
Tu ne l'as peut être pas remarqué, mais ton résultat :
est l'équivalent du résultat de ton corrigé :
Merci infiniment pour votre aide, encore une fois!
Je comprends beaucoup mieux désormais. De plus, je n'avais pas fait la correspondance entre mon résultat et le résultat de la correction...C'est plus clair 
Cependant, je rencontre encore un problème à une question de cet exercice (décidément il me cause beaucoup de tort celui-la):
Je vous récapitule mes avancements:
→ Étude du mouvement entre C et D.
5) Faire l'inventaire des forces qui s'exercent sur le wagonnet.
-Voici ce que j'ai trouvé:
►Son poids vertical;
►La réaction de la piste;
►La force , responsable du déplacement du wagon.
-Voici ce que le corrigé à écrit:
►Son poids vertical;
►La réaction de la piste, perpendiculaire à la piste;
Pourquoi la force n'est plus présente, une fois le wagon situé entre C et D? En effet, étant donné que les forces
et
s'annulent, une autre force doit forcément être responsable du fait que le wagon se déplace entre C et D; J'aurais justement imaginé que le vecteur
, placé vers la direction du vecteur
soit la source de ce déplacement... Mais bref; ce problème n'est pas ma plus grosse difficulté actuellement.
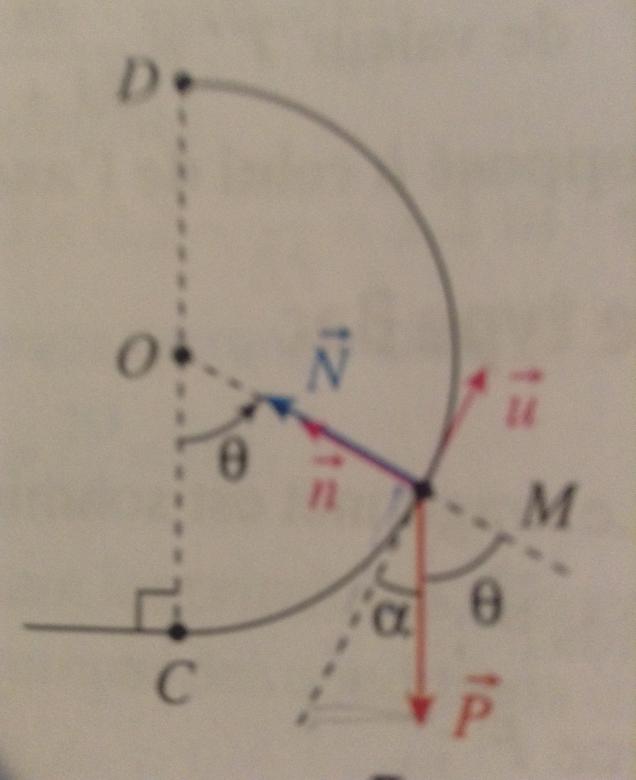
6) Appliquer la deuxième loi de Newton et la projeter dans le repère de Frenet. En déduire les expressions de et
en fonction de m, g, N (valeur de la réaction de la piste) et de l'angle
 .
.
-Voici ce que j'ai trouvé:
Grâce à la deuxième loi de Newton, .
On a ici un mouvement non uniforme, donc:
Projetons sur le repère de Frenet:
►Pour :
Nous projetons sur
, donc:
comme cos( ) =
) = , soit -P = -m*g*cos(
 )
)
Or, cos(90° -  ) = sin(
) = sin( )
)
Donc, = -m*g*sin(
 )
)
Soit = -g * sin(
 )
)
►Pour :
Nous projetons sur
, donc:
Comme cos( ) =
) = , alors N = -p * cos(
 )
)
Ce qui donne: m * = -m*g*cos(
 ) + N
) + N
Par conséquent, = -g * cos(
 ) +
) +
Cependant, je bloque sur le 7):
7)Montrer que l'expression v² - vc2 = 2g * R * cos( - 1) est en accord avec l'expression de
- 1) est en accord avec l'expression de trouvée dans la question précédente.
Comment faire pour arriver à ce résultat?
Je suppose qu'il faut dériver cette vitesse pour obtenir l'accélération, mais je ne trouve pas la valeur du corrigée, qui est:
Comment obtenir ce résultat?
Merci d'avance!
Question 5 :
L'énoncé dit clairement que la force s'exerce entre A et B.
Il n'est donc pas étonnant qu'elle ne figure plus entre C et D.
Le wagonnet lancé par la force entre A et B poursuit sa route sur sa lancée.
Question 7 :
En dérivant par rapport au temps l'expression :
V²-(Vc)² = 2gR(1 - cos(θ)) on trouve bien l'expression proposée par ton corrigé :
Or dθ/dt = V/R .... Je te laisse conclure.
Bonsoir,
Merci beaucoup encore une fois pour votre réponse!
D'accord, je comprends mieux pour la question 5;
Malheureusement je bloque toujours pour dériver l'expression: v² - v2c= 2g * R * cos( - 1)
- 1)
Pour moi, cette expression est présentée sous la forme (u * v)' = u'*v + u*v' avec:
u' = 2
u = 2gR
v = (cos( ) - 1)
) - 1)
v' = - sin( )
)
Ainsi, j'obtiens: 2V - 2Vc = 2 * cos( - 1) + 2gR - sin(
- 1) + 2gR - sin( )
)
Cela ne correspond évidemment pas au résultat de la correction. De plus, je ne sais pas ce que représente 2Vc (Que veut dire l'indice c ?)
Merci d'avance
Tout d'abord rectifie ton expression à dériver :
Ce n'est pas
V² - ( Vc )² = 2 * g * R * cos (θ-1)
mais
V² - ( Vc )² = 2 * g * R * (cos (θ) - 1) ou bien si on préfère :
V² - ( Vc )² = 2 * g * R * cos (θ) - 2 * g * R
Vc est la vitesse au point C : C'est une constante
g et R sont aussi des constantes.
V et θ sont les variables à dériver.
La dérivée de V² est 2V. dV/dt ( En maths on écrit cela 2V . V' )
La dérivée de cos (θ) = - sin (θ). dθ/dt ( En maths on écrit cela -sin(θ) . θ')
La dérivation donne donc :
2 V . dV/dt - 0 = 2 * g * R * ( - sin (θ). dθ/dt ) soit après simplification :
V . dV/dt = - g * R * sin (θ). dθ/dt