Inscription / Connexion Nouveau Sujet
Mécanique : masse du soleil
Bonjour,
J'ai un exo est je ne vois pas comment le commencer.
On considère de manière général le mouvement de corps satellisés (masse m) autour d'un astre central (masse M). Le rayon de l'orbite supposé circulaire est noté R, le rayon de l'astre central supposé sphérique est est noté r et l'altitude à partir de son sol est notée h.
1) Exprimer vecteur F en fonction de M, R est vecteur N . Appliquer la 2 loi de Newton. En déduire l'expression littérale du vecteur accélération a en fonction de M, R et vecteur N dans le cas d'un mouvement circulaire.
2) Montrer en posant l'expression générale de a qu'un mouvement circulaire dû à la gravitation est forcément uniforme. En déduire l'expression de la vitesse v en fonction de M et R
3) Exprimer après avoir déterminer l'expression de la circonférence d de l'orbite en fonction de R, la période de révolution T du corps satellisé.
4) Démontrer la 3é loi de Kepler. Montrer que l'étude du mouvement du corps satellisé permet de connaitre la masse M de l'astre central.
5) Pour trois planètes au chois sauf Pluton, rechercher la valeur de T et la valeur moyenne de R pour chacune d'entre elles. Déterminer les 3 valeurs correspondant à la masse du soleil. Proposer une valeur pertinente.
6) En déduire la vitesse des 3 planètes
7) Galilé pensait qu'un boulet de canon, tiré horizontalement du haut d'une colline pourrait tourner autour de la terre et revenir à son point de départ s'il était lancé avec une vitesse v suffisante. Expliquer pourquoi la réalisation de sont expérience est une utopie.
Calculer la vitesse théorique de v qu'il évoquait.
Données: Mterre= 5.98.1024 kg rterre = 6380 km
J'ai directement bloqué sur la 1) car je ne vouis pas la formule a utiliser j'ai celle-ci :
F=G*(M*m)/R²
Et donc je ne vois pas comment je pourrais remplacé le G dans se cas la.
Quelle qu'un peut il m'aider ?
Merci
donc pour
Donc sa donne :
Ou je me trompe ?
Je vois pas se que l'on me demande dans la 2 se qu'il faut faire j'ai oublié de préciser que c'est dans un repère de Frénet.
Pour la question deux j'ai mis l'expression suivante :
Mais avec cela je ne vois pas comment je peut montrer que le mouvement est uniforme car je ne sais pas si la vitesse est constante.
tu y es presque.
tu as deux expressions de l'accélération a (qui est un vecteur) donc écris l'égalité des composantes de ce vecteur et tu auras ta réponse (ici la base est (T,N) )
Merci de ta réponse
L'égalité donne :
J'avais oublié le N dans le post du dessus Mais avec cela je ne vois pas commence simplifier pour montrer que le mouvement circulaire est uniforme.
attention à l'orientation de la normale (N)
si N est orienté vers l'extérieur (comme ton expression de F l'indique)
a = dv/dt T - v2/R N (accélération centripète)
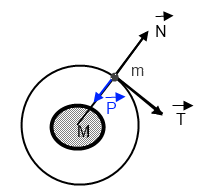
Donc dans mon expression de F il faut que je supprime le - si la normal est dirigé vers l'interieur et donc l'expression serait donc :
et
Mais avec cela je ne vois toujours pas comment traiter la question 2.
si N est dirigée vers l'intérieur (vers l'astre) on a effectivement:
a = dv/dt T + v2/R N
a = GM/R2 N
c'est une égalité vectorielle, donc tu écris que les composantes du vecteur a dans la base (T,N) sont uniques
d'où ...
je te mets sur la piste:
a = GM/R2 N s'écrit aussi a = 0 T + GM/R2 N
Donc on peut en déduire que : dv/dt = 0
Et que v est donc constant donc on a bien un mouvement circulaire uniforme.
Mais avec cela si la vitesse est constante comment puis-je l'exprimer en fonction de M et R
Faut-il appliquer la 2nd loi de newton?
Merci
C'est bon j'ai trouvé j'ai aussi fait la question 3
v=  ((GM)/R)
((GM)/R)
d=2piR et T= d/v
Maintenant J'ai a démontrer la 3é loi de Kepler question 4 mais je vois pas comment la démontrer je connais la formule qui est :
\frac{T^2}{R^3}=k
Je vois pas comment je pourrais assemblé les réponse précédente pour démontrer cela.
la 3e loi de Kepler dit que T2 est proportionnel à R3
donc calcule T2 en fct des données du problème (G,M,R), et essaie de voir si T2 / R3
est bien constant
Alors j'ai :
J'ai l'impression que mon calcule a foiré quelle que part sinon avec cela je vois mal comment mettre R au cube
T^2=\frac{d^2}{v^2}=\frac{4\Pi^2R^2}{\frac{GM}{R} }= \frac{4\Pi^2R^3}{GM}
Et donc on retombe mieux sur le T²/R3
Et donc on retombe mieux sur le T2/R3
Désolé j'avais oublié les balise
a l'aide de cette formule je vais pourvoir faire la question suivante .


 2/ (GM) = constante
2/ (GM) = constante
