Inscription / Connexion Nouveau Sujet
Mecanique des fluides
Bonjour, j'aurais besoin de votre aide pour résoudre cet exercice
Un écoulement d'huile de graissage de viscosité dynamique moyenne ? = 0,275 Pa.s et de masse volumique ? = 890 kg.m-3 se fait dans un tube horizontal de diamètre nominal DN = 150 mm et de longueur L = 120 m. On installe sur ce tube, deux capteurs de pression statique constitués par deux manomètres de Bourdon (PI Pressure Indicator sur le schéma) ; les valeurs des pressions relatives données par ces appareils sont : p2 = 1,12 bar et p3 = 0,465 bar.
patm = pression atmosphérique = 10^5 Pa, g = 9,81 m.s-2
1- Calculer la différence de pression  p23 = p2 - p3 en utilisant la loi de Poiseuille et en déduire la valeur du débit-volume qv puis la vitesse moyenne v du fluide dans le tube.
p23 = p2 - p3 en utilisant la loi de Poiseuille et en déduire la valeur du débit-volume qv puis la vitesse moyenne v du fluide dans le tube.
2- En déduire la valeur du nombre de Reynolds Re. Montrer qu'il s'agit bien d'écoulement laminaire.
3- Calculer la valeur du coefficient de perte de charge linéaire  .
.
Donner la valeur numérique du produit coeff de perte de charge *Re. Conclusions.
*Re. Conclusions.
4- Exprimer la relation de Bernoulli ; quelles sont les conditions d'application ?
Appliquer la relation de Bernoulli entre les points 1 et 2 en négligeant tout frottement entre ces deux points (notamment au point A).
En déduire l'expression littérale donnant H en fonction de patm , p2, v, ? et g. Calculer numériquement H.
Schéma de l'installation :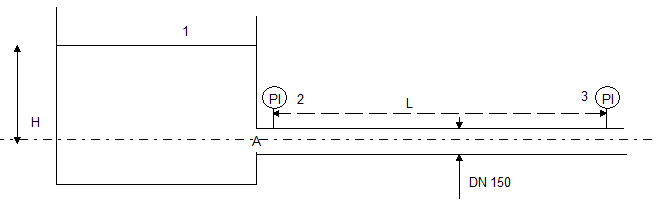
Merci d'avance
***Edit gbm : niveau mis en accord avec le profil***
Salut,
Il manque des notations dans ton problème (remplacés étrangement par des "?" ...).
Ensuite, où en es-tu ? Qu'as-tu fait ?

Désolé,
 = 0,275 Pa.s et de masse volumique
= 0,275 Pa.s et de masse volumique  = 890
= 890
En déduire l'expression littérale donnant H en fonction de patm , p2, v,  et g
et g
Reponse
1- P= P2-P3
P= P2-P3
=1.12 105-0.465
105-0.465 105
105
= 0.665 1
1
la lois de Poiseuille :  P = [(8
P = [(8
 L)/
L)/ .R4 ] . qv
.R4 ] . qv
on a :  =0.275 Pa.s \ L = 120m \ R =d/2 avec d= 150m \
=0.275 Pa.s \ L = 120m \ R =d/2 avec d= 150m \  P = 0.665
P = 0.665 105
105
on determne Qv :
 P = [(8
P = [(8
 L)/
L)/ .R4 ] . qv
.R4 ] . qv
 Qv =(
Qv =(  P
P 
 .R4 ) / (8
.R4 ) / (8
 L)
L)
= (0.655 105
105 

 754 ) / 8
754 ) / 8 0.275
0.275 120
120
donc Qv = 2.4 1010 m/s
1010 m/s
on trouve C la vitesse moyenne du fluide dans le tube :
on sait que : Qv = S C
C
 C = Qv/S
C = Qv/S
avec Qv= 2.4 1010 m/s et S=
1010 m/s et S= 
 d² / 4 (d= 150m)
d² / 4 (d= 150m)
donc: C= 2.4 1010 m/s / (
1010 m/s / ( 
 150²) / 4
150²) / 4
= 1.44  106
106
2- Re= C d/
d/
on calcule en premier la viscosité cinematique 
 =
=  /
/
avec  = 0.275Pa.s \
= 0.275Pa.s \  = 890 kg/m3
= 890 kg/m3
 = 0.275/890
= 0.275/890
= 3.1  10-4
10-4
on calcule Re
Re = 1.40 150/3.1
150/3.1  10-4
10-4
= 7 10-3
10-3
Re 2000
2000
donc l'ecoulement est laminaire
3- calcule de  coef de perte de charge
coef de perte de charge
puisque l'ecoulement est laminaire :  = 64/Re
= 64/Re
= 64/7 10-3
10-3
 = 9185.185
= 9185.185
4- theoreme de Bernoulli entre 1 et 2 en negligeant toutes les pertes :
w1-2= 1/2(C2² -C1²)+( P2-P1)/ +g(z2-z1)
p1=105 et z1=0 (je crois )
et je suis bloquée ici je sais pas cmment continuer , la meme chose pour Q5
(désole je suis nulle en organisation )
Merci
Hé bien, sans revoir en détail les applications numériques, ça m'a l'air pas mal tout ça  !
!
Quelques remarques :
1- P= P2-P3
P= P2-P3
=1.12 105-0.465
105-0.465 105
105
= 0.665 1 --> quelle est l'unité de ce résultat ? Une application numérique sans unité n'a pas de valeur.
1 --> quelle est l'unité de ce résultat ? Une application numérique sans unité n'a pas de valeur.
La loi de Poiseuille :  P = [(8
P = [(8
 L)/
L)/ .R4 ] . qv
.R4 ] . qv
on a :  =0.275 Pa.s \ L = 120m \ R =d/2 avec d= 150m \
=0.275 Pa.s \ L = 120m \ R =d/2 avec d= 150m \  P = 0.665
P = 0.665 105
105
--> as-tu vérifié que tout est dans les unités SI ?
on determne Qv :  P = [(8
P = [(8
 L)/
L)/ .R4 ] . qv
.R4 ] . qv Qv =(
Qv =(  P
P 
 .R4 ) / (8
.R4 ) / (8
 L)
L)
= (0.655 105
105 

 754 ) / 8
754 ) / 8 0.275
0.275 120
120
donc Qv = 2.4 1010 m/s
1010 m/s
--> ne change pas de notation en cours de route (Qv ou qv mais pas les deux) ;
--> m/s est relatif à une vitesse, et non à un débit volumique (m3/s) ;
--> attention aux unités : si tu veux avoir des m3/s, il faut convertir tous les paramètres en unités SI. Par exemple, j'ai l'impression que tu as fait une erreur dans le rayon de la conduite (75 --> en mm et non en m).
Reprends ce calcul posément, et n'hésite pas à critiquer l'ordre de grandeur.
on trouve C la vitesse moyenne du fluide dans le tube :
on sait que : Qv = S C
C C = Qv/S
C = Qv/S
avec Qv= 2.4 1010 m/s et S=
1010 m/s et S= 
 d² / 4 (d= 150m)
d² / 4 (d= 150m)
donc: C= 2.4 1010 m/s / (
1010 m/s / ( 
 150²) / 4
150²) / 4
= 1.44  106
106
--> pas d'unité ? Si ce sont des m/s, un jugement critique te permet de constater qu'une huile (visqueuse) allant à une telle vitesse dans la conduite la déformerait et la casserait très rapidement 
--> reprends le calcul à tête reposée, tu as la bonne méthode, tu as juste fait une faute d'inattention
2- Re= C d/
d/
on calcule en premier la viscosité cinematique 
 =
=  /
/
avec  = 0.275Pa.s \
= 0.275Pa.s \  = 890 kg/m3
= 890 kg/m3
 = 0.275/890
= 0.275/890
= 3.1  10-4
10-4
on calcule Re
Re = 1.40 150/3.1
150/3.1  10-4
10-4
= 7 10-3
10-3
Re 2000
2000
donc l'ecoulement est laminaire
--> calcul à reprendre suite à faute d'inattention en amont.
3- calcule de  coef de perte de charge
coef de perte de charge
puisque l'ecoulement est laminaire :  = 64/Re
= 64/Re
= 64/7 10-3
10-3 = 9185.185
= 9185.185
--> calcul à vérifier suite à faute d'inattention. Quelle unité ?
4- theoreme de Bernoulli entre 1 et 2 en negligeant toutes les pertes :
w1-2= 1/2(C2² -C1²)+( P2-P1)/ +g(z2-z1)
p1=105 et z1=0 (je crois )
et je suis bloquée ici je sais pas cmment continuer , la meme chose pour Q5
(désole je suis nulle en organisation )
--> on reviendra à cette question une fois que tu auras repris tous les calculs.
Ici il faut supposer que la vitesse v1 en surface est négligeable par rapport à la vitesse v2 en début de conduite.
P1 = Patm je présume
P2 est donné dans l'énoncé
la vitesse dans la conduite (donc v2) tu dois la recalculer.
Mercii !
Correction :
1-P= P2-P3
=1.12 105-0.465
105-0.465 105
105
 P=0.665
P=0.665 105 Pa
105 Pa
la lois de Poiseuille : P = [(8
 L)/.R4 ] . Qv
L)/.R4 ] . Qv
on a : =0.275 Pa.s \ L = 120m \ R =d/2 avec d= 150mm= 0.15m \ P = 0.665  105 Pa
105 Pa
la lois de Poiseuille : P = [(8
 L)/
L)/ .R4 ] . Qv
.R4 ] . Qv
on a : =0.275 Pa.s \ L = 120m \ R =d/2 avec d= 150mm= 0.15 m\ P = 0.665105
on determne Qv :
P = [(8
 L)/
L)/ .R4 ] . Qv
.R4 ] . Qv
Qv =(  P
P 
 .R4 ) / (8
.R4 ) / (8
 L)
L)
= (0.655 105
105 

 0.0754 ) / 8
0.0754 ) / 8 0.275
0.275 120
120
donc Qv = 2.5 10-2 m3/s
10-2 m3/s
on trouve C la vitesse moyenne du fluide dans le tube :
on sait que : Qv = S C
C
C = Qv/S
avec Qv= 2.5 10-2 m3/set S=
10-2 m3/set S= 
 d² / 4 (d= 150mm =0.15m)
d² / 4 (d= 150mm =0.15m)
donc: C= 2.5 10-2 / (
10-2 / ( 
 0.15²) / 4
0.15²) / 4
= 1.41 m/s
2- Re= Cd/
on calcule en premier la viscosité cinematique
 =
= /
/
avec = 0.275Pa.s \ = 890 kg/m3
= 0.275/890
= 3.1 10-4
on calcule Re
Re = 1.41 0.15/3.1
0.15/3.1 10-4
10-4
= 684.49
Re  2000
2000
donc l'ecoulement est laminaire
3- calcule de coef de perte de charge
puisque l'ecoulement est laminaire : = 64/Re
= 64/684.49
= 0.093
En un coup d'oeil, une vitesse d'écoulement du fluide à 1,41 m/s est du bon ordre de grandeur.
Du coup la 4 ?

4- W1-2 = 1/2(C2²-C1²)+P2-P1/ +g(z2-z1)+
+g(z2-z1)+ Jl+
Jl+ Js
Js
Pertes de charge négligés et pas d'echange d'energie ( pas de machine hydraulique ) donc W1-2 = 0
1/2(C2²-C1²)+P2-P1/ +g(z2-z1) = 0
+g(z2-z1) = 0
1/2(1.41)+(1.12 105)-0.465
105)-0.465 10[sup]5[/sup
10[sup]5[/sup 10[sup]5[/sup ] /9.81+g(z2-z1)
10[sup]5[/sup ] /9.81+g(z2-z1)
Je sais pas comment continuer
Entre 1 et 2, on peut négliger les pertes de charge --> on revient au théorème de Bernoulli classique
De toute façon, on te demandait de calculer la perte de charge entre 2 et 3, et non entre 1 et 2 :
1/2(C2²-C1²) + (P2-P1)/p +g.(z2 - z1) = 0
z2 - z1 = H
or je t'avais dit qu'on faisait l'hypothèse suivante : la vitesse en surface de la bâche est négligeable devant celle du fluide en 2 donc v1 << v2 <=> v1  0
0
soit
1/2C2² + (P2-Patm)/p +gH = 0
si je suppose qu'on est dans les conditions atmosphériques en surface (P1 = Patm) et P2 fournie par l'énoncé.

Mercii
1/2C2² + (P2-Patm)/ +gH = 0
+gH = 0
 gH = -1/2C2² - (P2-Patm)/
gH = -1/2C2² - (P2-Patm)/
H = [-1/2C2² - (P2-Patm)/ ] / g
] / g
= [-1/2 * 1.41² -(1.12*105 - 105 )/890 ] / 9.81
= | -1.47 |
= 1.47 m



