Inscription / Connexion Nouveau Sujet
Mécanique d'un objet sur un plan incliné
Bonsoir j'ai une activité en cinématique à faire mais je n'arrive pas à terminer la deuxième partie merci de votre aide.
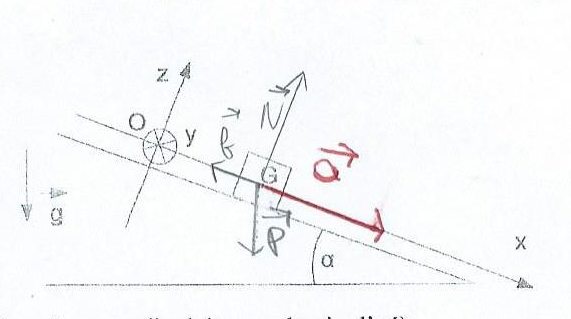
On considère un objet de masse m qui glisse (avec frottement) le long de la ligne de la plus grande pente d'un plan incliné faisant un angle 
avec l'horizontale. Le repère de projection Oxyz est fixe dans le référentiel terrestre (Ox est selon la ligne de la plus grande pente du plan incliné orienté vers le bas, Oy est horizontal et perpendiculaire à Ox, Oz est perpendiculaire au plan incliné).
A) Etude des graphiques
Dans cette partie on a deux graphiques :
- x = f(t)
- Vx = f(t)
j'ai tout réussi il fallait en étudiant les graphes donner la valeur de x et Vx à t=0s puis en déduire selon les courbes si l'objet remontait ou descendait la pente, dans notre cas il fait les deux à t=2s
Puis il fallait déterminer la valeur de l'accélération x qui vaut 3/2 (j'ai retrouvé l'équation de la courbe de la vitesse et je l'ai dérivé)
B) Etude théorique
Dans cette question, l'objet est en mouvement vers le bas le long de la ligne de la plus grande pente du plan incliné. L'objet est soumis à une force de frottement (de valeur constante et colinéaire et de sens contraire au vecteur vitesse de l'objet). En appliquant la seconde loi de Newton
1. Déterminer le vecteur accélération de l'objet en fonction de m, g, et f ; représenter, sans souci d'échelle, ce vecteur sur le schéma ci-dessus.
Pour cette question j'ai démontré la 2nde loi de Newton où on retrouve m.a = m.g sauf que je n'arrive pas à trouver les valeurs du vecteur accélération. Je sais qu'il faut faire avec les projections sinus, cosinus etc ..
Merci d'avance
B)
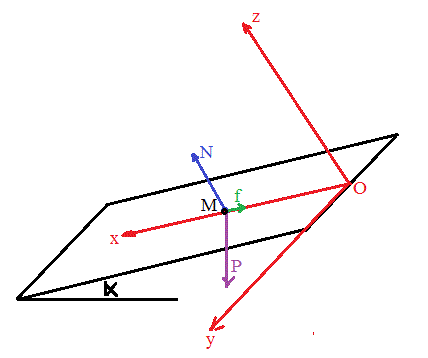
Le mobile est soumis à 3 forces :
- Son Poids : P (vertical vers le bas)
- Une composante de la réaction du support normale à la piste (vers le haut) : N
- L'ensemble des forces de frottement : f (direction du déplacement mais de sens contraire)
La projection de ces 3 forces sur l'axe Ox donne: P.sin(alpha) - f + N*cos(90°) = mg.sin(alpha) - f
La composante de l'accélération suivant ox est notée ax est est telle que : mg.sin(alpha) - f = m.ax
ax = g.sin(alpha) - f/m
La projection de ces 3 forces sur l'axe Oy donne : P.cos(90°) + N.cos(90°) + f.cos(90°) = 0 et donc ay = 0
Comme le mobile reste sur le plan incliné pendant la descente, on a z = 0 sur tout le parcours et donc az = 0
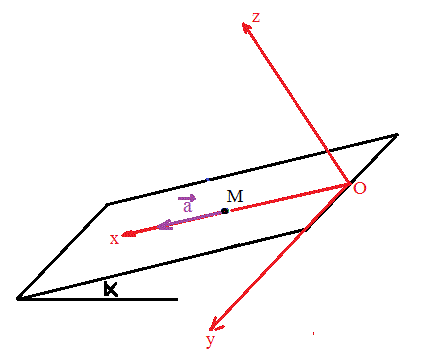
Le vecteur accélération a donc pour coordonnées : (g.sin(alpha) - f/m ; 0 ; 0)
Sauf distraction. 
Merci beaucoup pour la réponse bien détaillé. Hier soir j'avais réussi à trouver g.sin -f/m aussi mais je n'étais pas sûre. Je vais maintenant essayer de rrépondre aux questions suivantes merci beaucoup bonne journée 
; P.cos90°) ?
Bonjour j'ai eu une seconde question sur cet énoncé
2) déterminer l'expression de la valeur de la réaction normale du support sur l'objet en fonction de m,g et
Comme vous l'aviez fais j ai pris les coordonnées de N (N.cos90°; N.cos90°) sauf que je ne vois pas comment utiliser m g et alpha..
En projetant les forces (N,P et f) sur un axe perpendiculaire au plan incliné (donc parallèle à l'axe oz) :
N - P.cos(alpha) = 0
N = mg.cos(alpha)
vecteur N(0 ; 0 ; mg.cos(alpha))
-----
Sauf distraction.
Annuler
connectez vous