Inscription / Connexion Nouveau Sujet
Mécanique classique
J'ai un exercice que j'ai eu en devoir que je n'arrive pas à résoudre entièrement malgré mon cours...
Le problème est le suivant : La position ( en mètre ) d'un point M dan le plan est donné en fonction du temps ( s ) par les équations paramétriques x(t)=3cos(2t) y(t)=3sin(2t)
(i) Calculez les composantes du vecteur vitesse et du vecteur accélération. Calculez les modules de ces vecteurs. Sont ils indépendants du temps ?
v(x)=dx/dt= -6sin(2t) a(x)= -12cos(2t)
v(y)=dy/dt= 6cos(2t) a(y)= -12sin(2t)
/v/= (-6sin(2t))²+(6cos(2t))² = 6 car sin²(2t)+cos²(2t)=1
/a/= (-12cos(2t))²+(-12sin(2t))² = 12
Ils sont indépendants du temps comme on a juste des nombres entiers ( 6 et 12 ) ( je ne sais pas si cette réponse correspond )
( ii ) Montrez que la distance de M à l'origine est constante. La trajectoire est un cercle dont on déterminera le rayon R. On peut aussi repérer la position du point M par l'angle 
(t). Ecrire la relation (t). En déduire la vitesse angulaire et l'accélération angulaire.
Pour calculer la distance OM je calcule son module que je note r :
/r(t)/=3, le module est indépendant de t donc la distance de M à l'origine est constante, je sais pas du tout si c'est ça qu'il faut répondre...
Après je ne vois pas le "dont on déterminera le rayon R", on doit attendre la suite de l'exercice pour le déterminer ou on doit le déterminer maintenant ?
Ecrire la relation (t) : cos=Ox/OM et là je sais pas trop que faire, dire que cos= et donc =Ox/OM=R/OM ? Mais on me parle de en fonction de t ? Je m'embrouille surement.
Pour la vitesse angulaire si je continue dans ce sens je sais que 
=d/dt= ??? Je ne sais pas du tout dans quel sens aller là, OM est une constante, R aussi, donc w=R*OM ?
Accélération angulaire : 
=d/dt=d²/dt= R*OM ??
(iii) En utilisant (i) retrouvez la relation qui existe entre le module de la vitesse, le rayon et la vitesse angulaire, puis la relation qui existe entre le module de l'accélération et vitesse et rayon.
Pour répondre à cette question il faut déjà que je valide les réponses précédentes...
Merci beaucoup de votre aide 
Edit Coll : suppression de balises
bonsoir,
tu y es presque!
Ils sont indépendants du temps comme on a juste des nombres entiers ( 6 et 12 )
oui, en fait il faut dire que |v| et |a| étant des constantes (pas forcément des entiers!), ils sont indépendants du temps
/r(t)/=3, le module est indépendant de t donc la distance de M à l'origine est constante,
il suffit de dire: |OM| = 3 donc |OM| est constant.
à ton avis, quel est l'ensemble des points vérifiant: |OM| = 3 ?
oui R = 3 m
On peut aussi repérer la position du point M par l'angle
(t). donc tu connais x en fonction de R et de
, idem pour y (cf schéma)
et par identification avec l'équation horaire:
x(t)=3cos(2t)
y(t)=3sin(2t)
tu en déduis
(t)
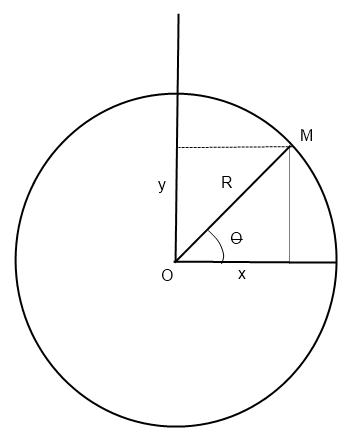
D'accord, donc x=R et y=R
Et donc 3cos(2t)=R ce qui donne =3cos(2t)/R
3sin(2t)=R ce qui donne =3sin(2t)/R
C'est cela ?
Merci de votre aide en tout cas !
Et pour la fin ? En utilisant (i) retrouvez la relation qui existe entre le module de la vitesse, le rayon et la vitesse angulaire, puis la relation qui existe entre le module de l'accélération et vitesse et rayon.
Je sais w=v/R... Mais je ne vois pas comment le démontrer. J'ai le module de la vitesse /v/=6, R=3 et w=2 ce qui montre que la relation est juste mais c'est pas ce qu'on me demande ?
Idem pour l'accélération...
Merci beaucoup de vos réponses.
iii) on te demande de vérifier la relation, pas de la démontrer
v = R w est bien vérifiée ici puisque 3x2 = 6
pour l'accélération je te laisse terminer
Mais moi je comprends "en utilisant (i) retrouver la relation",il me semble que à la fin du devoir il a dit que ceux qui avait "vérifier" aurait faux...
Pourtant je comprends "en utilisant (i) retrouver la relation", il me semble qu'à la fin du devoir mon professeur ait dit que ceux qui avait "vérifié" aurait faux....
oui, peut-etre
x(t) = R cos O(t)
y(t) = R sin O(t)
donc
x'(t) = -R O' sin O(t)
y'(t) = R O' cos O(t)
ici O' = w = cste
donc en calculant |v| = 
( x' 2 + y' 2) on retrouve: v = R w
Sinon pour l'accélération je connais une relation a=v²/r mais je ne vois pas comment la démontrer ici, et a n'est pas le module...
J'ai fait comme vous sinon en faisant le module de a, j'ai trouvé seulement quelque chose comme /a/=*R, avec l'accélération angulaire. Il faut que j'intègre un v... Je cherche mais je ne vois pas.
on a:
x(t) = R cos O(t)
y(t) = R sin O(t)
donc
x'(t) = -R O' sin O(t)
y'(t) = R O' cos O(t)
tu calcules simplement x"(t) et y"(t) et tu retrouveras l'accélération centripète bien connue
|a| = ( x" 2 + y" 2) = ...
Mais je le fais mais je comprends pas du tout, je trouve /a/=RO" mais pourquoi je pourrais dire que O"=v²/r², ça sort d'où ? J'aime pas utiliser des formules sans les comprendre... Qui est O" ?
x'(t) = -R O' sin O(t)
y'(t) = R O' cos O(t)
donc
x"(t) = -R O' 2 cos O(t)
y"(t) = -R O' 2 sin O(t)
donc |a| = R O' 2 = V2 /R (car V = R O' )
Annuler
connectez vous