Bonsoir
Lors d'une expérience de diffusion par effet Compton, la longueur d'onde λ' des
photons diffusés selon un angle θ est donnée par la relation :
λ-λ'=(h/me*c)*(1 - cos θ)
λ : longueur d'onde des photons incidents (m) ; me : masse de l'électron cible (kg) ; h : constante de Planck ; c : célérité de la lumière dons le vide
La longueur d'onde des photons diffusés est de 71,0 pm pour un angle θ = 90°.
1- Calculer la langueur d'onde des photons incidents.
2- Calculer la valeur du vecteur quantité de mouvement d'un photon incident et d'un photon diffusé.
3- Écrire la relation traduisant la conservation de la quantité de mouvement du système {photon-électron}, l'électron
cible étant considéré comme libre et immobile avant le choc.
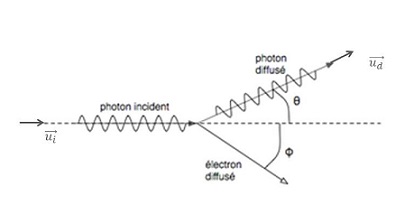
4- Réaliser un schéma indiquant les vecteurs quantités de mouvement avant la collision et après la collision dans le cas où θ = 90°.
En déduire la valeur du vecteur quantité de mouvement de l'électron après la collision et la valeur de l'angle φ, angle que fait ce vecteur avec la direction du photon incident.

Je bloque à la 3, pouvez-vous m'aider svp