Inscription / Connexion Nouveau Sujet
mécanique
Bonjour j'aimerais avoir de l'aide :
Une voiture de masse m=1000kg, assimilée à un point matériel roule à 83,5km/h sur une route rectiligne en pente descendante, faisant un angle de 4,0° avec l'horizontale. A partir d'une position A de la voiture, le conducteur freine brutalement. Il s'arrête à la position B au bout de 50m.
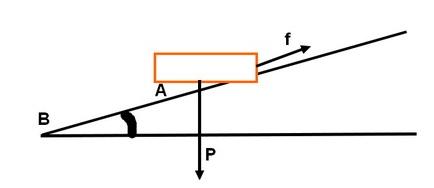
a) présenter sur un schéma les forces qui agissent sur la voiture
b) Donner l'expression de la variation d'énergie mécanique de la voiture pendant le freinage
c) Calculer la valeur de la force de freinage f.
j'ai fait :
a)
b) Em=Epp+Ec mais entre les points A et B ?
c)
merci
Bonjour,
Il faut calculer la variation d'énergie cinétique :
(puisque v est nulle à l'état final)
Il faut calculer la variation d'énergie potentielle :
(détant la distance sur le plan incliné ==> 50 m)
et :
" (détant la distance sur le plan incliné ==> 50 m) " ==> (d étant la distance sur le plan incliné ==> 50 m)
ok donc :
a) ok
b) Em=-1/2mv²-mgdtan =-1/2*1000*23-1000*9,81*50*tann4
=-1/2*1000*23-1000*9,81*50*tann4
c'est ça ?
c) comment calculer f?
OK pour b ==> v = 23,2 m/s ( 83,5 ==> 3 chiffres significatifs )
c)
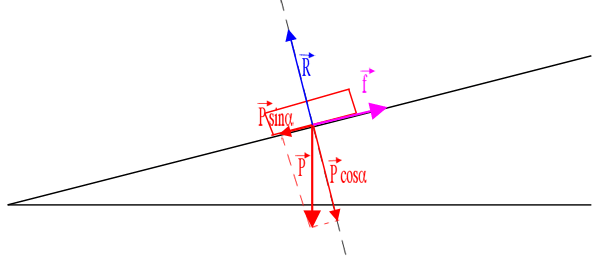
On a :
Et, selon le plan incliné, on a :
On a donc :
et on a
sinon la voiture ne s'arrête pas...
Donc la résultante est orientée vers le haut du plan incliné. Son travail est donc résistant donc négatif :
et on a :
Comme , on a finalement :
b)
En prenant l'altitude du point B comme référence pour les énergies potentielles de pesanteur nulles:
Energie mécanique en A : EmA = (1/2).m.VA² + mg.AB.sin(alpha)
Energie mécanique en B : EmB = 0
Delta Em = EmB - EmA
Delta Em = - (1/2).m.VA² - mg.AB.sin(alpha)
---
c)
Delta Em = f * AB
f * AB = - (1/2).m.VA² - mg.AB.sin(alpha)
f = - (1/2).m.VA²/AB - mg.sin(alpha)
f = -(1/2) * 1000 * (83,5/3,6)²/50 - 1000 * 9,81.sin(4°)
f = -6,06.10^3 N
---
Sauf distraction. 


